1 소수의 중요성¹

소수는 그리스 시대부터 본인과 1로만 나눠줘서 절대 깨지지 않는 합성수와 다른 완전성 때문에 큰 관심을 갖게 되었다. 즉, 합성수는 소수의 곱으로 인수분해를 통해 구할 수 있기 때문에 소수를 알게 되면 모든 숫자를 이해하게 되는 것이라 여겨졌다. 소수는 수(자연수)의 근원이다.

정수론 혹은 수론(Number Theory)에서 소수는 중요한 의미를 갖는다. 역사적으로 중요한 소수에 대한 상식적인 내용은 다음과 같다.

에라토스테네스의 체: 고대 그리스 수학자 에라토스테네스가 발견한 소수를 찾는 방법
가우수 소수 정리(Prime number theorem): 소수의 분포를 근사적으로 기술하는 정리로 어떤 큰 수 \(N\) 에 가까운 정수 하나를 무작위로 골랐을 때 그 정수가 소수일 확률은 \(\displaystyle \frac {1}{\ln N}\) 에 근사한다는 것을 보여 준다. 달리 표현하면, 어떤 양수 이하의 소수가 몇 개나 있는지 그 값을 어림해주는 정리다. 어떤 양수 \(x\)에 대해 \(x\)보다 작은 소수의 개수는 대략 \(\frac{x}{\log x}\)개가 있다고 주장하는 정리이다.
리만 가설: 리만은 1859년 “주어진 수보다 작은 소수의 개수에 관하여” 라는 제목의 논문을 출간하였다. 논문은 임의의 양의 정수 N이 아주 클 경우 N까지의 소수의 수가 로그 적분 함수에 점근한다는 가설을 고찰하였다. 이를 위해서 오일러가 제시한 제타함수를 사용하였다.

\[Li(N) = \int_{0}^{N} {\frac{1}{\log x}}dx\]

2 에라토스테네스의 체

에라토스테네스의 체는 고대 그리스 수학자 에라토스테네스(Eratosthenes)가 발견한 소수를 찾는 알고리즘이다.

일단 1을 지우자.
2를 제외한 2의 배수를 지우자.
3을 제외한 3의 배수를 지우자.
4의 배수는 지울 필요 없다.(2의 배수에서 이미 지워졌다)
2, 3 다음으로 남아있는 가장 작은 소수, 즉 5의 배수를 5를 제외하고 지우자.
마지막으로 7을 제외한 7의 배수까지 지운다.
8의 배수는 지울 필요 없다.(2의 배수에서 이미 지워졌다.) 9의 배수도 지울 필요 없다.(3의 배수에서 이미 지워졌다.) 10의 배수도 지울 필요 없다.(2의 배수에서 이미 지워졌다.)
11의 배수부터는 \(11 > \sqrt{100}\) 이기 때문에 역시 지울 필요 없다.
- \(n\)까지 모든 수의 배수를 다 나눌 필요는 없다. 어떤 수 \(m=ab\)라면 \(a\) 와 \(b\) 중 적어도 하나는 \(\sqrt{n}\)이다.

sieve_of_eratosthenes <- function(num){
  values <- rep(TRUE, num)
    values[1] <- FALSE
    prev_prime <- 2
    for(i in prev_prime:sqrt(num)){
        values[seq.int(from = 2 * prev_prime, to = num, by = prev_prime)] <- FALSE
        prev_prime <- prev_prime + min(which(values[(prev_prime + 1) : num]))
    }
    return(which(values))
}

sieve_of_eratosthenes(10)

[1] 2 3 5 7

소수를 생성하는 R 팩키지는 다음과 같다.

library(schoolmath)
library(primefactr)
library(sfsmisc)
library(primes)
library(numbers)
library(spuRs)
library(randtoolbox)
library(matlab)

numbers 팩키지를 사용해서 10까지 소수를 찾아보자.

library(numbers)

numbers::Primes(n1 = 10)

[1] 2 3 5 7

3 소수는 무한하다.

유클리드(Euclid)에 의해서 “소수는 무한히 많다”라는 사실이 증명되었다. 과연 그럴까 다음 가정을 기반으로 증명해보자.

모든 자연수는 소수가 아니면 합성수다.
소수는 자기자신과 1이 아니면 나눠지지 않는다.
합성수는 모두 소수의 곱으로 인수분해될 수 있다.

산술의 기본 정리(fundamental theorem of arithmetic)는 모든 양의 정수는 유일한 소인수 분해를 갖는다는 정리이다. 예를 들어, 1200은 다음과 같이 소수의 곱으로 표현되는데 순서를 바뀌는 것을 제외하면 유일하다.²

\[1200 = 2^4 \cdot 3 \cdot 5^2 = (2 \cdot 2 \cdot 2 \cdot 2) \cdot 3 \cdot (5 \cdot 5) = 5 \cdot 2 \cdot 5 \cdot 2 \cdot 3 \cdot 2 \cdot 2 = \ldots\]

상기 사실을 근거로 소수는 무한히 많다는 사실을 증명할 수 있다.

단계: 소수는 소수의 곱(\(2 \cdots p\))을 써서 표현할 수 있다. 즉, \(N = 2 \cdot 3 \cdot 5 \ldots p\).
단계: \(N\) 보다 1이 큰 수가 있다고 가정하자. 즉, \(N +1 = 2 \cdot 3 \cdot 5 \cdots p + 1\).
단계: \(N +1\)이 합성수라고 가정하면 산술의 기본정리에 의해 소수 \(2 \cdots p\) 중 하나에 의해 나눠지게 됩니다. 하지만, 1이 있기 때문에 결국 자기 자신으로만 나눠지게 되어 \(N +1\)가 합성수라는 가정은 부정되고 소수가 됩니다.
단계: 따라서, 1 단계에서 정의한 소수 \(N\) 보다 큰 소수는 항상 존재하게 되어 “소수는 무한히 많다”가 성립하게 됩니다.

4 가우스 소수 정리

어떤 양수 \(x\)에 대해 \(x\)보다 작은 소수의 개수는 대략 \(\frac{x}{\log x}\)개가 있다는 것을 표로 정리하면 다음과 같다. 즉, 1~10 사이는 2,3,5,7 소수가 4개 1~100 사이는 25개 … 와 같이 정리된다.

library(tidyverse)
library(rvest)

prime_number_theorem_url <- "https://en.wikipedia.org/wiki/Prime_number_theorem"

Sys.setlocale("LC_ALL", locale = "C")

[1] "C"

gauss_tbl <- prime_number_theorem_url %>% 
  read_html(encoding = "UTF-8") %>% 
  html_nodes(xpath = '//*[@id="mw-content-text"]/div[1]/dl[53]/dd/table') %>% 
  html_table(fill = TRUE, header = TRUE) %>% 
  .[[1]] %>% 
  select(1,2,4)

Sys.setlocale("LC_ALL", locale = "Korean")

[1] "LC_COLLATE=Korean_Korea.949;LC_CTYPE=Korean_Korea.949;LC_MONETARY=Korean_Korea.949;LC_NUMERIC=C;LC_TIME=Korean_Korea.949"

gauss_tbl %>% 
  as_tibble() %>% 
  mutate(x = as.character(x)) %>% 
  mutate(power = str_remove(x, pattern = "10")) %>% 
  mutate(power = ifelse(power > 0, power, 1) %>%  as.integer) %>% 
  mutate(x = 10 ** power) %>% 
  reactable::reactable()

5 소수의 갯수

자연수 \(N\)까지 포함된 소수의 갯수를 세어보자. 이를 그래프로 만들어 시각화한다.

library(numbers)
library(tidyverse)

count_prime_numbers <- function(num) {
  Primes(num) %>% length
}

numbers_seq <- 2:10000

prime_tbl <- tibble(numbers       = numbers_seq,
                    prime_numbers = map_int(numbers_seq, count_prime_numbers))

prime_tbl %>% 
  ggplot(aes(x= numbers, y=prime_numbers)) +
    geom_line() +
    geom_point(size = 0.1) +
    theme_light() +
    labs(title = "자연수 N 까지 소수의 갯수",
         x     = "자연수",
         y     = "소수의 갯수") +
    scale_x_continuous(labels = scales::comma) +
    scale_y_continuous(labels = scales::comma)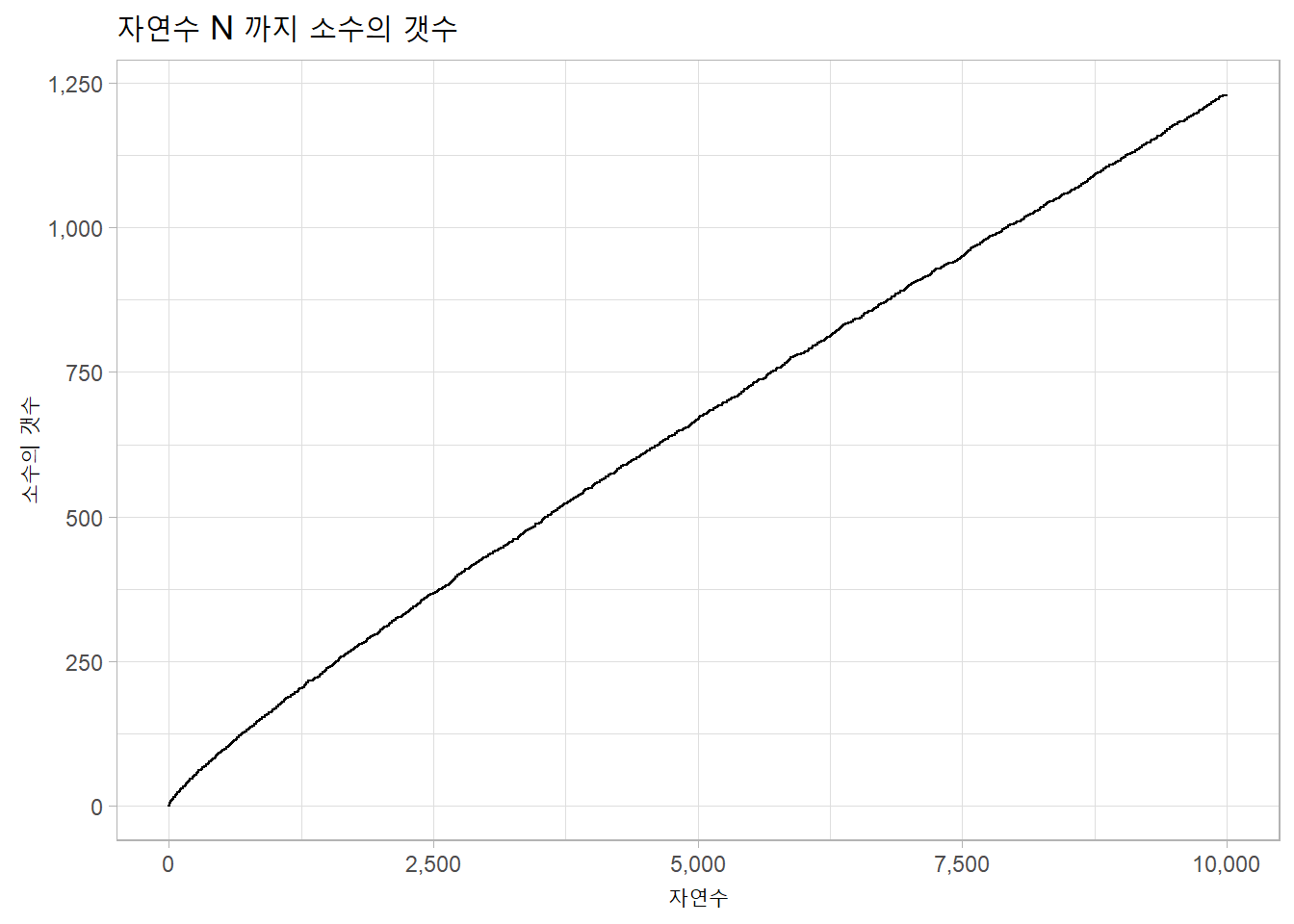

데이터 과학자 이광춘 저작

kwangchun.lee.7@gmail.com

기호 수학(Symbolic Math)

소수(Prime Number)

이광춘

2021-02-11

1 소수의 중요성¹

2 에라토스테네스의 체

3 소수는 무한하다.

4 가우스 소수 정리

5 소수의 갯수

기호 수학(Symbolic Math)

소수(Prime Number)

이광춘

2021-02-11

1 소수의 중요성1

2 에라토스테네스의 체

3 소수는 무한하다.

4 가우스 소수 정리

5 소수의 갯수

1 소수의 중요성¹