1 기하 기호

기하학에서 자주 사용되는 수학기소는 다음과 같다.

의미	수학기호	$\LaTeX$
선분(Line Segment)	$\overline{\rm AB}$	\overline{\rm AB}
각(Angle)	$\angle$	\angle
측정된 각(Measured Angle)	$\measuredangle$	\measuredangle
삼각형(Triangle)	$\triangle$	\triangle
정사각형(Square)	$\square$	\square
합동( congruent ): 같은 모양, 크기	$\cong$	\cong
닮음(similar, same shape)	$\sim$	\sim
평행(is parallel with)	$\\|$	\\|
수선(perpendicular): 어떤 일정한 직선 또는 평면에 수직인 직선	$\perp$	\perp

2 다양한 수학 도형¹

\begin{tikzpicture}
  \begin{scope}[blend group = soft light]
    \fill[red!30!white]   ( 90:1.2) circle (2);
    \fill[green!30!white] (210:1.2) circle (2);
    \fill[blue!30!white]  (330:1.2) circle (2);
  \end{scope}
  \node at ( 90:2)    {Statistics};
  \node at ( 210:2)   {Mathematics};
  \node at ( 330:2)   {Coding};
  \node [font=\Large] {Data Science};
\end{tikzpicture}

$Funky tikz$

Funky tikz

2.1 직각 삼각형

tikz $\LaTeX$ 팩키지를 사용해서 직각삼각형을 그려보자.

\begin{tikzpicture}[scale=1.25]

    \coordinate [label = left:$C$]  (A) at (0,0);
    \coordinate [label = right:$A$] (C) at (3,0);
    \coordinate [label = above:$B$] (B) at (3,3);
    
    \draw             (A) --
    node[above] {$a$} (B) --
    node[right] {$c$} (C) -- 
    node[below] {$b$} (A);
    
    \draw (3, 0) rectangle (2.7, 0.3);

\end{tikzpicture}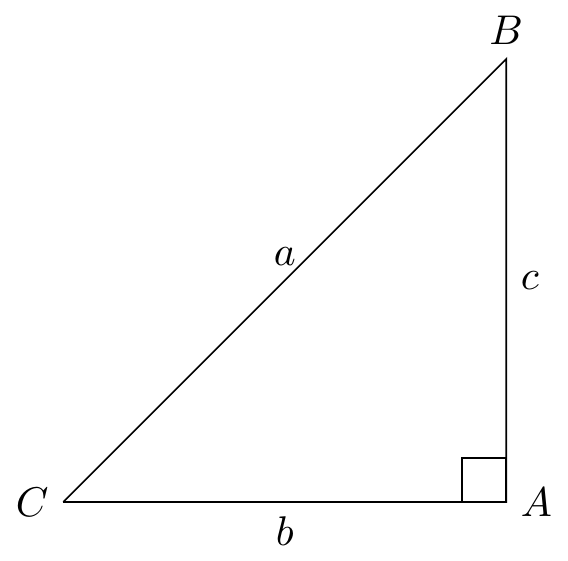

상기 tikz $\LaTeX$ 코드 대신 삼각형을 ggplot으로 그려보자. geom_segment(), geom_point()를 사용하여 기하도형을 그리고 annotate()로 삼각형의 기호를 표시한다.

library(tidyverse)

ggplot() +
  # 선분 AB, BC, CA
  geom_segment(aes(x=0, y = 0, xend = 3, yend = 0)) +
  geom_segment(aes(x=3, y = 0, xend = 3, yend = 3)) +
  geom_segment(aes(x=3, y = 3, xend = 0, yend = 0)) +
  # 점 A, B, C
  geom_point(aes(x=0, y=0), size = 3) +
  geom_point(aes(x=3, y=0), size = 3) +
  geom_point(aes(x=3, y=3), size = 3) +
  # 점에 라벨 붙이기
  annotate("text", x = 0, y= 0, label = "C", hjust =  2, size = 5) +
  annotate("text", x = 3, y= 0, label = "A", hjust = -1, size = 5) +
  annotate("text", x = 3, y= 3, label = "B", vjust = -1, size = 5) +
  # 선분에 라벨 붙이기
  annotate("text", x = 1.5, y = 0.0, label = "italic(b)", vjust =  1, size = 5, parse = TRUE) +
  annotate("text", x = 3.0, y = 1.5, label = "italic(c)", hjust = -1, size = 5, parse = TRUE) +
  annotate("text", x = 1.5, y = 1.5, label = "italic(a)", vjust = -1, size = 5, parse = TRUE) +
  # 직각 표시
  geom_segment(aes(x=2.9, y = 0.0, xend = 2.9, yend = 0.1)) +
  geom_segment(aes(x=2.9, y = 0.1, xend = 3.0, yend = 0.1)) +
  theme_void() +
  coord_equal(ratio = 1) +
  scale_x_continuous(limits = c(-0.5, 3.5)) +
  scale_y_continuous(limits = c(-0.5, 3.5))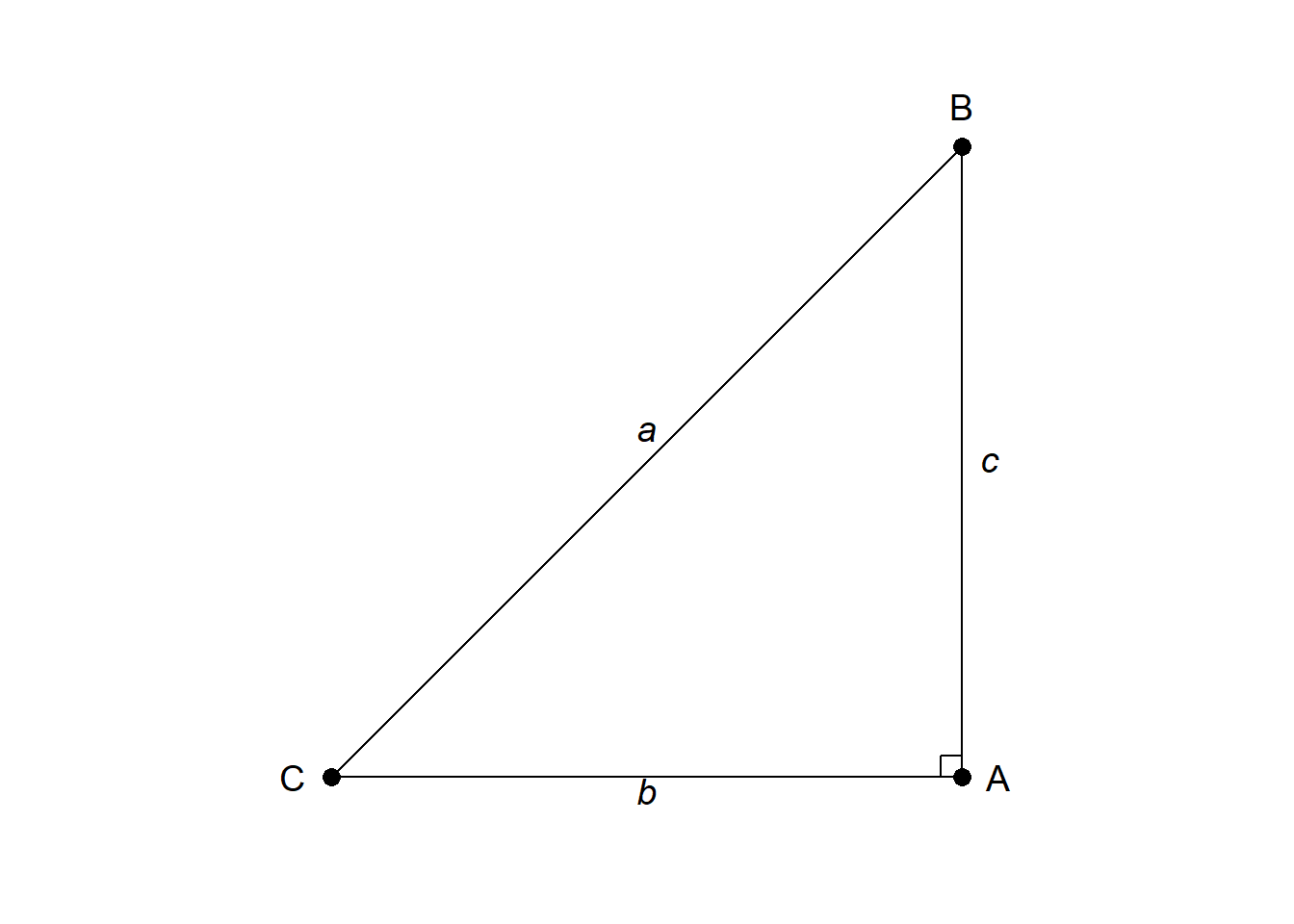

2.2 교차점 [^intersection-point]

$(-1,2)$, $(2,-4)$ 두점을 지나는 직선과 $(-1,-1)$, $(2,2)$ 두점을 지나는 직선이 교차하는 교차점 $(0,0)$을 tikz 팩키지로 구현해보자.

\begin{tikzpicture}
\draw[gray, thick] (-1,2) -- (2,-4);
\draw[gray, thick] (-1,-1) -- (2,2);
\filldraw[black] (0,0) circle (2pt) node[anchor=west] {Intersection Point};
\end{tikzpicture}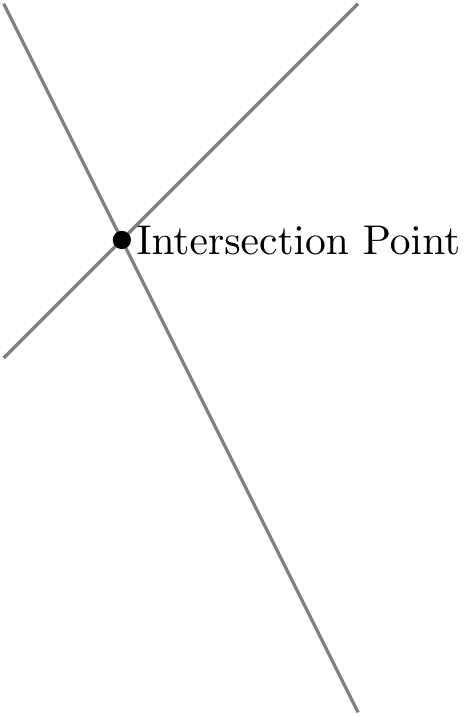

상기 tikz $\LaTeX$ 코드 대신 ggplot으로 시각화를 해보자. geom_segment()로 두 선분을 그리고 교차점을 geom_point()로 표식한다.

ggplot() +
  # 선분 AB, BC
  geom_segment(aes(x = -1, y =  2, xend = 2, yend = -4)) +
  geom_segment(aes(x = -1, y = -1, xend = 2, yend =  2)) +
  # 교차점
  geom_point(aes(x=0, y=0), size = 3, color = "midnightblue") +
  # 점에 라벨 붙이기
  annotate("text", x = 0, y= 0, label = "교차점", hjust =  -0.5, size = 5) +
  theme_minimal() +
  coord_equal(ratio = 1) +
  scale_x_continuous(limits = c(-4, 4)) +
  scale_y_continuous(limits = c(-4, 4)) +
  labs(x = "x 축", 
       y = "y 축")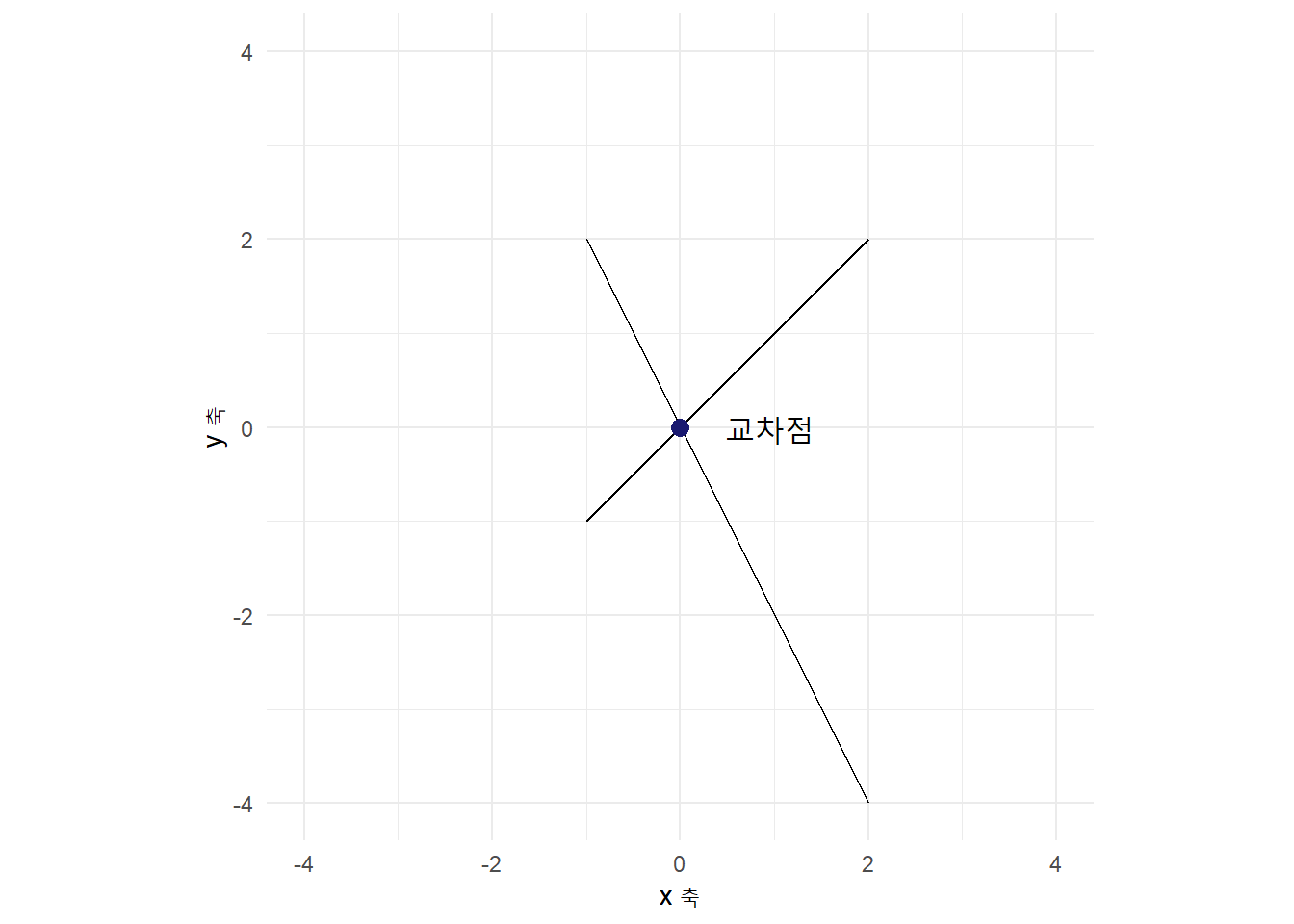

2.3 직사각형

두 점 $(0,0)$, $(1,2)$을 시작점과 끝점으로 삼아 rectangle 을 통해 직사각형을 그릴 수 있다.

\begin{tikzpicture}

\draw[step=1cm, gray, very thin] (-2,-2) grid (6,6);
\draw[blue, very thick] (0,0) rectangle (1,2);
\draw[red, very thick] (2,2) -- (5,2) -- (5,5) -- (2,5) -- cycle;
\draw[thick,->] (0,0) -- (6,0) node[anchor=north west] {x axis};
\draw[thick,->] (0,0) -- (0,6) node[anchor=south east] {y axis};
\foreach \x in {0,1,2,3,4,5}
   \draw (\x cm,1pt) -- (\x cm,-1pt) node[anchor=north] {$\x$};
\foreach \y in {0,1,2,3,4,5}
    \draw (1pt,\y cm) -- (-1pt,\y cm) node[anchor=east] {$\y$};

\end{tikzpicture}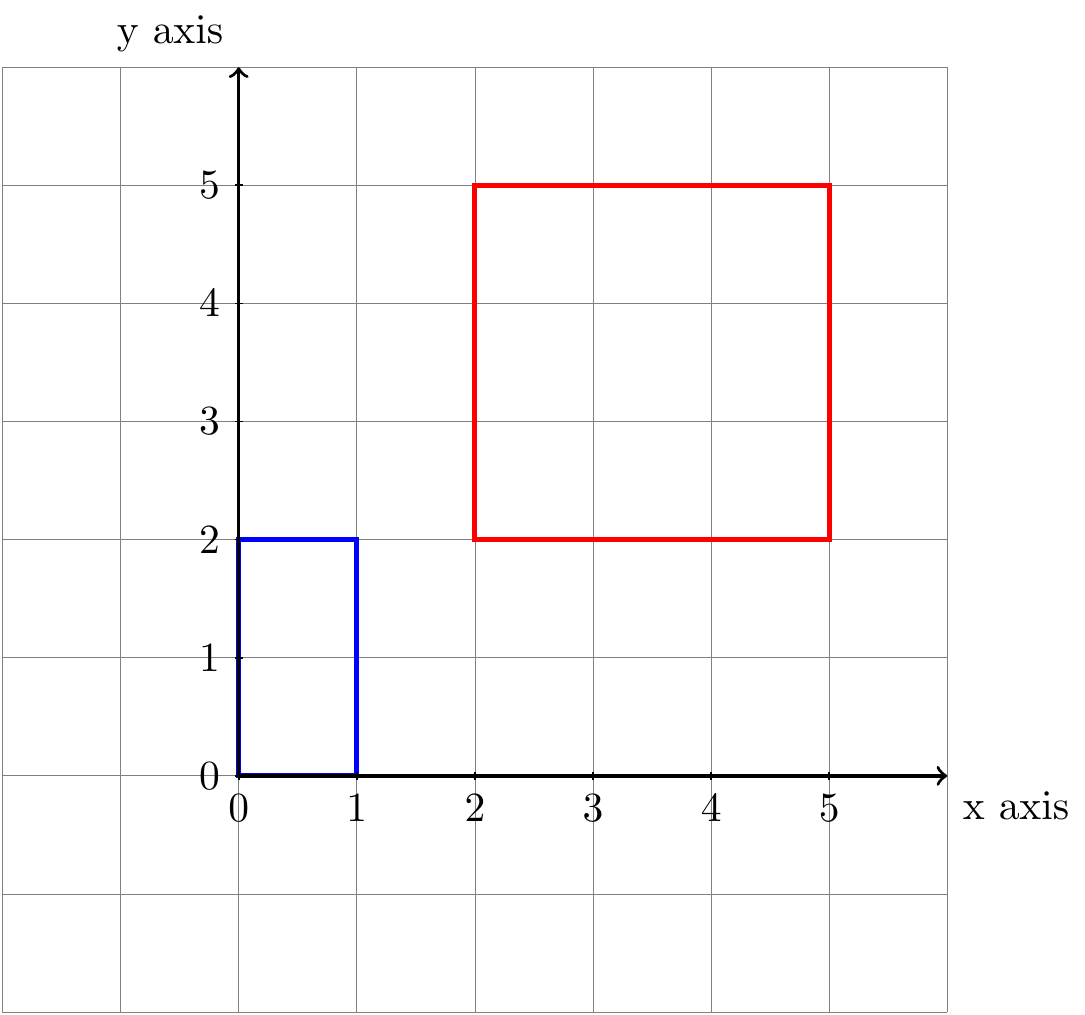

\usepackage{tkz-euclide} 팩키지를 활용하게 되면 좌표계를 기본으로 넣어 직사각형을 표현할 수 있다.

\begin{tikzpicture}
   \tkzInit[xmax=6,ymax=6,xmin=-1,ymin=-1] 
   \tkzGrid 
   \tkzAxeXY
        \draw[blue, very thick] (0,0) rectangle (1,2);
        \draw (2,2) -- (5,2) -- (5,5) -- (2,5) -- cycle;
  \tkzText[above](0,6.75){Draw Rectangle}
\end{tikzpicture}

상기 tikz $\LaTeX$ 코드 대신 ggplot으로 시각화를 해보자.

ggplot() +
  # 직사각형 
  geom_rect( fill=alpha("blue",0), alpha=0.7,
    aes(xmin = 0, ymin=0, xmax = 1, ymax=2)) +
  geom_rect( fill=NA, alpha=0.7, color = "red",
    aes(xmin = 2, ymin=2, xmax = 5, ymax=5)) +
  theme_minimal() +
  coord_equal(ratio = 1) +
  scale_x_continuous(limits = c(-1, 6)) +
  scale_y_continuous(limits = c(-1, 6)) +
  labs(x = "x 축", 
       y = "y 축")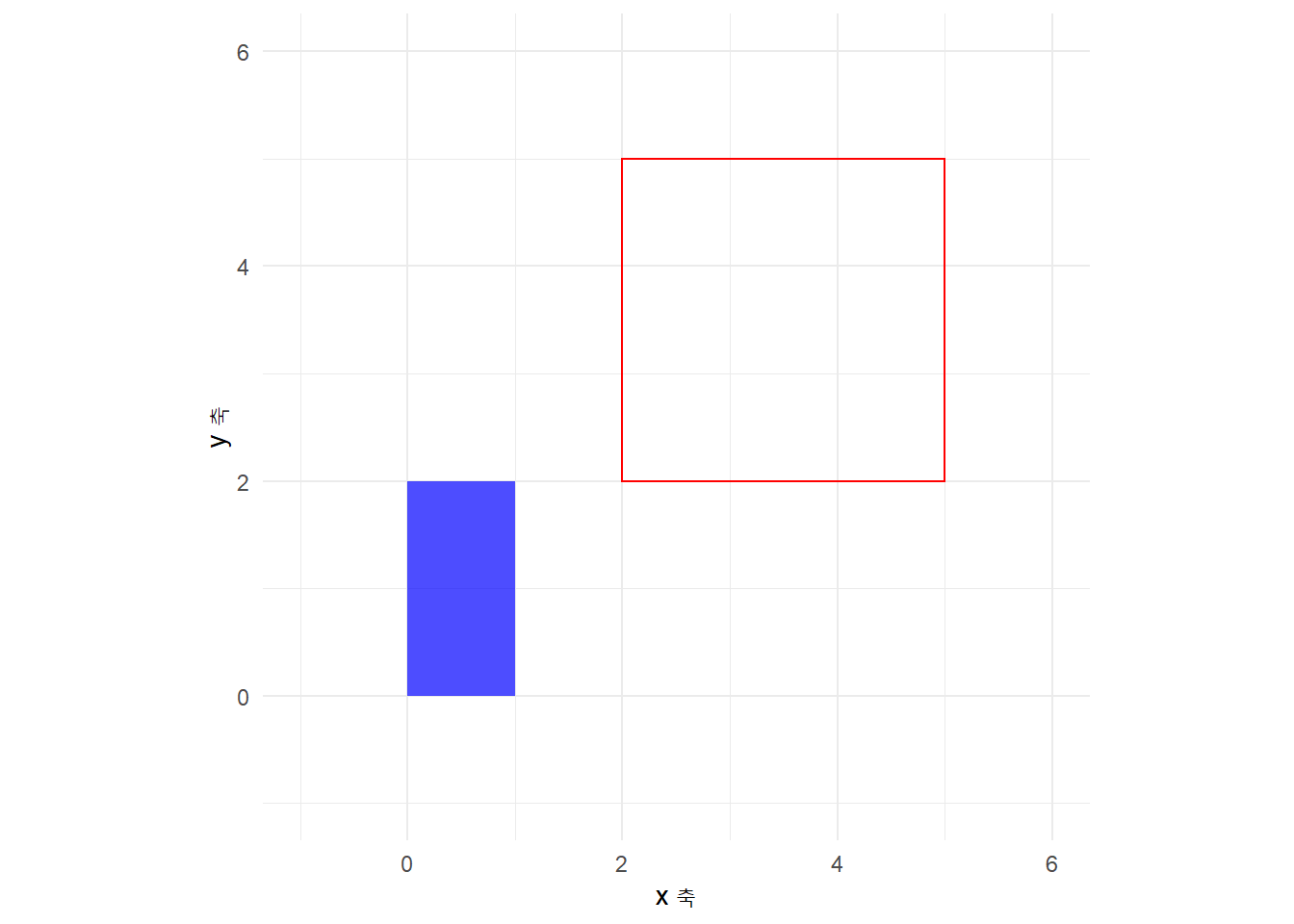

2.4 원

좌표계를 설정하여 tikz 팩키지로 그리는 도형을 쉽게 알 수 있도록 밑바탕을 두고 원(circle), 타원(ellipse), 호(arc)를 각각 그려보자. 먼저 검정색 원은 중심이 $(0,0)$이며 반지름이 2가 되도록 그려본다. 두번째 타원은 중심이 $(3,3)$ 이며, 장축이 3, 단축이 1이 되도록 작도한다. 마지막으로 호는 시작점이 $(0,0)$, $0^{\circ} \sim 270^{\circ}$가 되도록 하는데 반지름은 3으로 하여 작도한다.


\begin{tikzpicture}

\draw[thick,->] (0,0) -- (6,0) node[anchor=north west] {x axis};
\draw[thick,->] (0,0) -- (0,6) node[anchor=south east] {y axis};
\foreach \x in {0,1,2,3,4,5}
   \draw (\x cm,1pt) -- (\x cm,-1pt) node[anchor=north] {$\x$};
\foreach \y in {0,1,2,3,4,5}
    \draw (1pt,\y cm) -- (-1pt,\y cm) node[anchor=east] {$\y$};

\draw (0,0) circle (2cm);
\draw (3,3)[blue] ellipse (3cm and 1cm);
\draw (0,0)[red] arc (0:270:3cm);

\end{tikzpicture}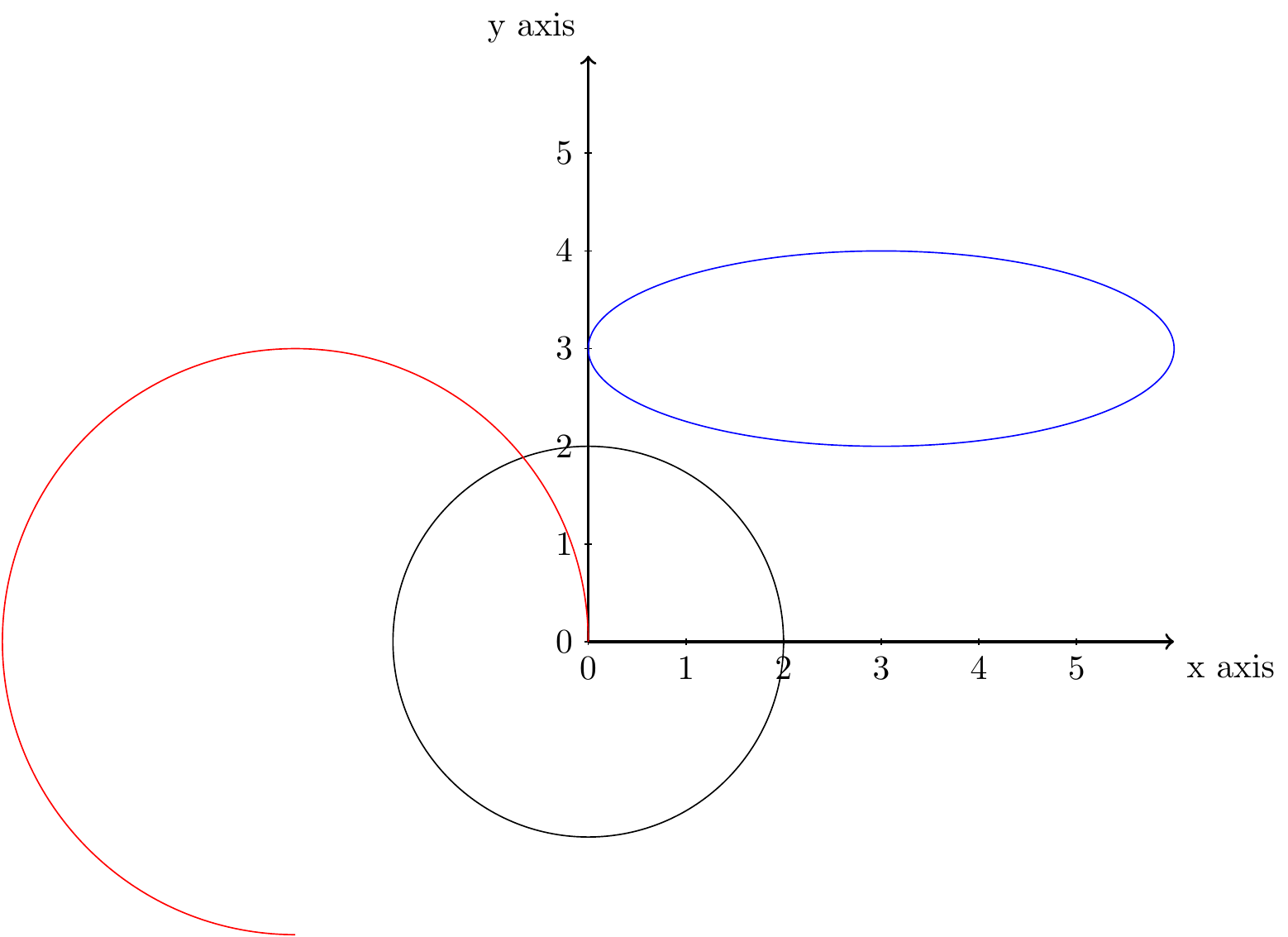

상기 tikz $\LaTeX$ 코드 대신 ggplot으로 시각화를 해보자. ggforce 팩키지 geom_circle()을 사용한다. geom_arc()를 사용하여 호도 시각화 시킬 수 있고, geom_ellipse()를 사용하게 되면 타원도 그릴 수 있다.

library(ggforce)

ggplot() +
  # 원
  geom_circle(aes(x0 = 0, y0 = 0, r = 2), color = "black") +
  # 호(Arc)
  geom_arc(aes(x0 = -3, y0 = 0, r = 3, start = pi / 2 , end = - pi ), color = "red", lineend = 'butt', size = 1) +
  # pi 위치
  annotate("text", x = 0, y = 3, label = "2 * pi", vjust =  1, size = 5, parse = TRUE) +
  annotate("text", x = -3, y = 0, label = "3 / 2 * pi", vjust =  1, size = 5, parse = TRUE) +
  annotate("text", x = 0, y = -3, label = " pi", vjust =  1, size = 5, parse = TRUE)  +
  # 타원 (ellipse)
  geom_ellipse(aes(x0 = 3, y0 = 3, a = 3, b = 1, angle = 0), color = "blue") +
  theme_classic() +
  coord_equal(ratio = 1) +
  scale_x_continuous(limits = c(-6, 6), breaks = seq(-6, 6, 1)) +
  scale_y_continuous(limits = c(-6, 6), breaks = seq(-6, 6, 1)) +
  labs(x = "x 축", 
       y = "y 축") +
  geom_hline(yintercept = 0) + 
  geom_vline(xintercept = 0)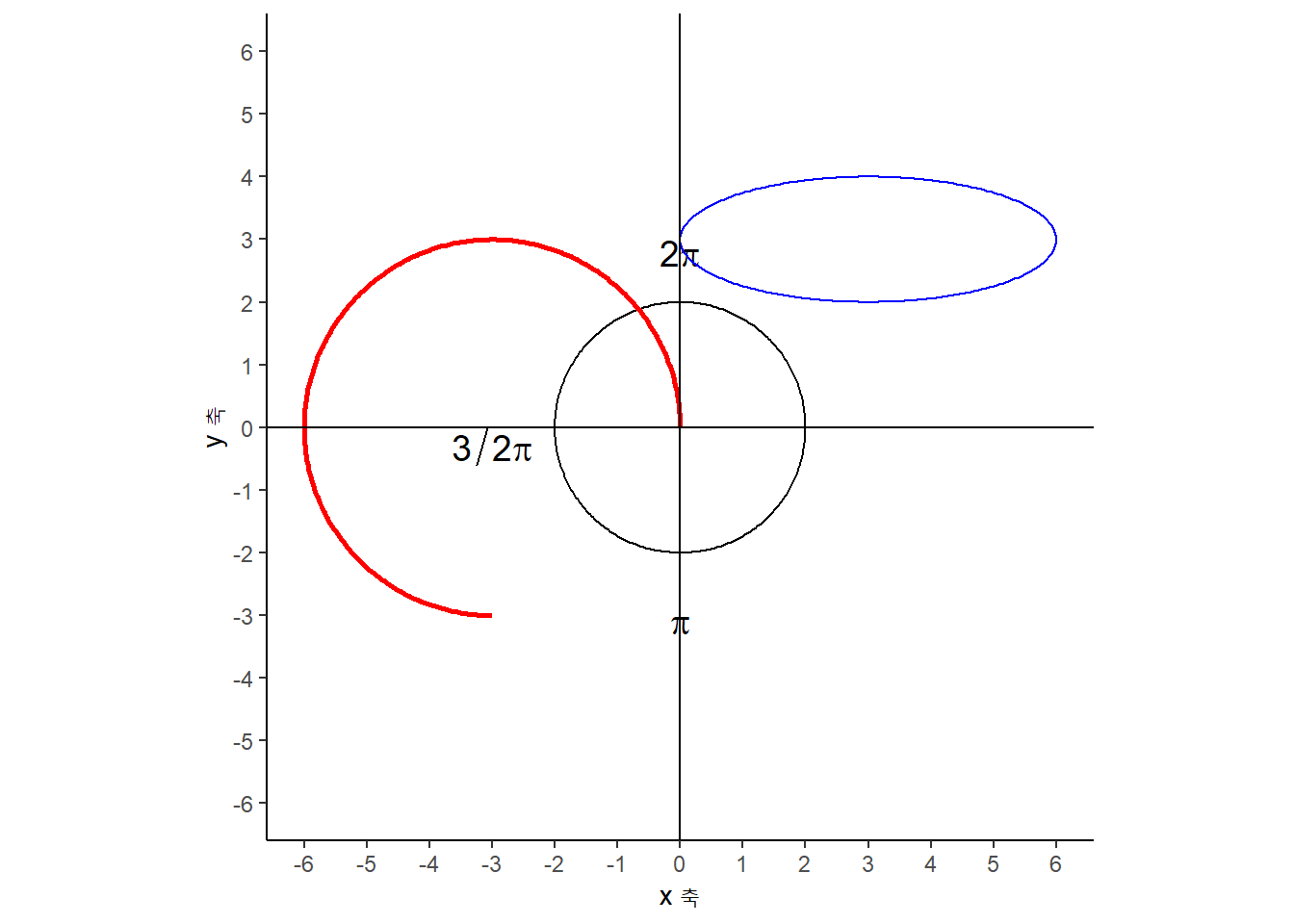

“How to force Tikz in RMarkdown document to show cyrillic text?”, stackoverf"↩︎

데이터 과학자 이광춘 저작

kwangchun.lee.7@gmail.com

기호 수학(Symbolic Math)

R마크다운 - 기하 저작

이광춘

2021-02-13

1 기하 기호

2 다양한 수학 도형¹

2.1 직각 삼각형

2.2 교차점 [^intersection-point]

2.3 직사각형

2.4 원

의미	수학기호	\(\LaTeX\)
선분(Line Segment)	\(\overline{\rm AB}\)	\overline{\rm AB}
각(Angle)	\(\angle\)	\angle
측정된 각(Measured Angle)	\(\measuredangle\)	\measuredangle
삼각형(Triangle)	\(\triangle\)	\triangle
정사각형(Square)	\(\square\)	\square
합동( congruent ): 같은 모양, 크기	\(\cong\)	\cong
닮음(similar, same shape)	\(\sim\)	\sim
평행(is parallel with)	\(\\|\)	\\|
수선(perpendicular): 어떤 일정한 직선 또는 평면에 수직인 직선	\(\perp\)	\perp

기호 수학(Symbolic Math)

R마크다운 - 기하 저작

이광춘

2021-02-13

1 기하 기호

2 다양한 수학 도형1

2.1 직각 삼각형

2.2 교차점 [^intersection-point]

2.3 직사각형

2.4 원

2 다양한 수학 도형¹