넘파이(Numpy)¶
파이썬은 네덜란드 출신 귀도 반 로섬이 1991년 교육용으로 C 언어와 유닉스 셀을 간극을 줄이려고 개발되었다. 파이썬은 과학기술을 위한, 웹 개발을 위한, 이미지 처리를 위한, 언어는 아니다. 파이썬이 주목받고 많이 사용되는 이유는 실행속도(speed of execution)가 좋기 때문이 아니라, 개발속도(speed of development)가 충분히 빠르기 때문이다.
과거에는 컴퓨터 시간(machine time)이 중요했으나, 컴퓨터가 너무 많고 흔해져 버린 지금에 와서는 개발자 시간(human time)이 중요하고, 희소한 자원이 되었다. 파이썬은 기존에 개발된 C/포트란 언어로 수십년동안 개발되고 검증된 소프트웨어를 현재 목적에 맞춰 래퍼(wrapper) 언어로 과학기술 컴퓨팅에 지대한 역할을 수행했다.
파이썬이 과학기술 컴퓨팅의 C/포트란 언어로 개발된 소프트웨어를 래퍼 언어로 기능을 확대함과 동시에 선형대수 행렬 처리를 위해 작은 데이터는 Numeric, 큰 데이터는 Numarray로 각기 개발진행되어 가다 NumPy 팩키지로 통합되어 현재 모습에 이르고 있다.
매트랩에 영감을 받아 Multipack을 거쳐 SciPy로 행렬기반 매트랩과 같은 통합팩키지로 개발되었고, 매쓰매티카에 영감을 받아 IPython 노트북이 개발되었으며, 시각화를 위해 matplotlib이 개발되고, 행렬에서 처리 못하는 결측값처리 및 통계 R에서 기본 자료구조로 사용되는 데이터프레임을 지원하는 Pandas가 개발되었고, 기계학습에 맞춰 scikit-learn 팩키지가 순차적으로 기존 개발된 것에 덧붙여 개발되었다. 너무 많은 팩키지가 개발되어 개발환경 격리와 팩키지 관리를 위해 conda도 개발되었다.
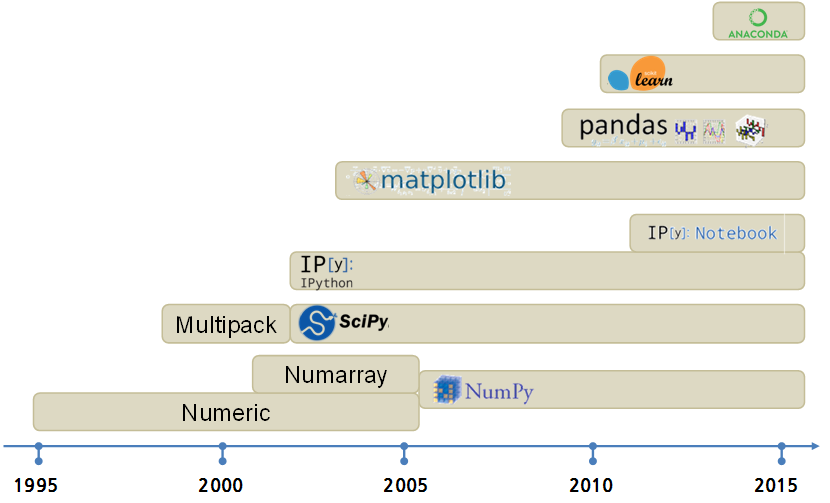
Numpy 팩키지는 파이썬 과학 컴퓨팅에서 데이터 분석, 기계학습, 딥러닝의 가장 기반이 되는 자료구조로 벡터와 행렬을 다루는데 있어 인지부하를 최소화하도록 해주는 역할이 크다. 대표적으로 scikit-learn, SciPy, pandas, tensorflow가 넘파이에 기반하고 있다.
참고자료: Jay Alammar, "A Visual Intro to NumPy and Data Representation"
import numpy as np
np.array([1,2,3])
np.ones(3)
np.zeros(3)
np.random.random(3)
배열연산¶
배열 연산은 선형대수에서 사용하는 수식을 참조하여 작성한다.
for 루프를 동원하여 각 원소별로 연산작업을 수행하는 코드를 작성하는 것과 비교하여 훨씬 인간적이다.
data = np.array([1,2])
ones = np.ones(2)
data + ones
data - ones
data * data
data / data
data * 1.6
인덱스(index)¶
1차원 배열에 저장된 원소를 끄집어내는 다양한 방법에 대한 인덱스(index) 연산자를 살펴보자
data = np.array([1,2,3])
data[0]
data[1]
data[0:2]
data[1:]
종합(aggregation)¶
배열을 하나의 숫자로 종합하는 다양한 메쏘드를 살펴본다.
.min(), .max(), .sum() 메쏘드 외에도 .mean() 평균, .std() 표준편차, .prod() 원소곱을 포함하여 다양한 종합 메쏘드가 존재한다.
data.max()
data.min()
data.sum()
다차원 배열¶
앞서 1차원 배열이 아니라 2차원 이상의 다차원 배열을 살펴보자. 1차원 배열을 모은 것을 행렬이라고 부른다.
행렬 생성¶
리스트로 앞서 1차원 배열을 구성했다면, 리스트를 묶은 리스트를 활용해서 행렬을 생성시킬 수 있다.
np.array([[1,2],[3,4]])
.ones(), .zeroes(), .random.random() 메쏘드 내부에 튜플로 행과 열을 지정하게 되면 행렬을 생성시킬 수 있다.
np.ones((3,2))
np.zeros((3,2))
np.random.random((3,2))
행렬연산¶
+-/* 4칙 연산자를 활용하여 두 행렬에 대한 연산을 가할 수 있다.
특히 행과 열이 맞지 않는 경우 브로드케스팅(broadcasting) 기능을 활용하여 연산을 수행한다. 이런 경우 Numpy 내부가 정한 연산에 대한 브로드케스트 규칙이 사용된다.
data = np.array([[1,2], [3,4]])
ones = np.ones((2,2))
data + ones
data = np.array([[1,2], [3,4], [5,6]])
ones_row = np.ones((1,2))
data + ones_row
내적 (dot product)¶
앞서 살펴본 행렬연산과 달리 두 행렬간의 내적은 다른 연산규칙을 따르기 때문에 두 행렬을 곱할 때 두행렬의 곱이 정의되도록 특히 신경을 쓴다. 예를 들어 $1 \times 3$ 행렬과 $3 \times 2$ 행렬을 곱하게 되면 $1 \times 2$ 행렬이 결과로 나오게 된다.
.dot() 메쏘드를 사용하여 두 행렬의 내적을 계산한다.
data = np.array([[1,2,3],])
powers_of_ten = np.array([[1,10], [100, 1000], [10000, 100000]])
data.dot(powers_of_ten)
행렬 색인(matrix indexing)¶
행렬의 원소에 접근하는데 [,]를 슬라이스 연산자와 함께 사용한다.
data = np.array([[1,2], [3,4], [5,6]])
data
data[0,1]
data[1:3]
data[0:2,]
행렬 종합(aggregation)¶
벡터와 마찬가지 방법으로 행렬에 대한 종합을 다양한 메쏘드를 활용하여 수행할 수 있다.
data.max()
data.min()
data.sum()
axis= 매개변수를 던져 행 혹은 열방향으로 데이터 종합값을 구할 수 있다.
axis=0는 세로 칼럼방향이고 되고, axis=1은 가로 행방향이 된다.
data = np.array([[1,2], [5,3], [4,6]])
data
data.max(axis=0)
data.max(axis=1)
전치와 모양바꿈(reshape)¶
행렬로 작업할 때 흔히하는 작업이 행렬의 행과 열을 바꾸는 전치(transpose)와 배열의 모양을 변형시키는 것이다.
data = np.array([[1,2], [3,4], [5,6]])
data
data.T
data = np.array([1,2,3,4,5,6])
data.reshape(2,3)
data.reshape(3,2)
N차원 차원 배열¶
넘파이를 사용해서 임의 차원에서 앞서 언급한 연산작업을 수행할 수 있는데 이런 경우 필요한 것이 ndarray 즉 N차원 배열이다.
np.array([
[[1,2], [3,4]],
[[5,6], [7,8]]
])
ones(), .zeros(), .random.random() 메쏘드에 추가로 튜플형태로 차원을 추가하면 ndarray를 생성시킬 수 있다.
A Visual Intro to NumPy and Data Representation에서 나온것과 차이가 나니 주의한다.
np.ones((2,4,3))
np.zeros((2,4,3))
np.random.random((2,4,3))
predictions = np.array([1,1,1])
labels = np.array([1,2,3])
error = (1/3) * np.sum(np.square(predictions - labels))
error
데이터 표현 - 데이터프레임¶
가장 일반적으로 정사각형 데이터프레임을 판다스로 표현한다.
import pandas as pd
df = pd.DataFrame({'Artist':['Billie Holiday','Jimi Hendrix', 'Miles Davis', 'SIA'],
'Genre': ['Jazz', 'Rock', 'Jazz', 'Pop'],
'Listeners': [1300000, 2700000, 1500000, 2000000],
'Plays': [27000000, 70000000, 48000000, 74000000]})
df.head()
소리 - 시계열¶
이미지¶
자연어¶
word embedding, BERT, ...