데이터 과학을 위한 R 알고리즘

요세푸스 문제(Josephus Problem)

1. 요세푸스가 겪은 일화

요세푸스 문제(Josephus problem, 혹은 Josephus permutation)은 실제 요세푸스가 겪은 일화에서 시작되었다. 로마시대 유대인들은 로마 지배에 봉기하여 맞서 싸웠지만 위기에 처하게 되자 명예로운 자결을 선택하였다.

요세푸스를 포함한 병사 총 41명이 원으로 둘러서서 3번째 사람을 죽여서 아무도 남지 않을 때까지 반복하고 나면, 마지막 사람은 스스로 자결하는 선택을 하는 결정을 하였다. 요세푸스를 포함한 병사 총 41명이 이런 결정에 동의를 했지만, 요세푸스 자신을 꼭 살고자 했다. 그럼 요세푸스는 몇번째 자리에 위치해야 모든 사람이 다 죽은 후에 홀로 살아남을 수 있을까?

예를 들어, 4명이 원을 둘러 처형하는 순서는 2 → 4 → 3 → 1 으로 도식으로 표현하면 다음과 같다. ¹

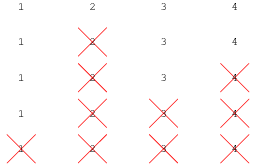
총 41명이 원으로 둘러서서 매 3번째 병사를 처형하는 순서는 다음과 같다.

3→ 6→ 9→ 12→ 15→ 18→ 21→ 24→ 27→ 30→ 33→ 36→ 39→ 1→ 5→ 10→ 14→ 19→ 23→ 28→ 32→ 37→ 41→ 7→ 13→ 20→ 26→ 34→ 40→ 8→ 17→ 29→ 38→ 11→ 25→ 2→ 22→ 4→ 35→ 16→ 31

2. 요세푸스 문제 점화식 ²

요세푸스 문제를 푸는 방법은 동적 프로그래밍(Dynamic Programming)을 활용하는 것이다. 인덱스가 1에서 시작한다고 가정하면, \(f(1,k)=1\) 초기항을 두고, 다음과 같은 점화식으로 표현할 수 있다.

\[f(n,k)=((f(n-1,k)+k-1) \bmod n)+1\]

3. R 코드

요세푸스 문제 점화식을 R코드로 재귀(Recursion)으로 표현하면 총 1 - 41 명까지 원으로 둘러선 경우를 가정하고, 매번 3번째 사람을 처형하는 경우 생존자를 모사하면 다음과 같다. 즉, 41명이 있는 경우 3번째 사람을 처형하는 경우 최종 생존자는 31번째 위치가 된다.

jesephus_rec <- function(people, passes) {
    if (people == 1) {
        return(1)
    }
    return((jesephus_rec(people-1, passes) + passes-1) %% people + 1 )
}

for(i in 1:41) {
    survivor <- jesephus_rec(i, 3)
    cat("병사수:", i, "생존자:", survivor, "\n")
}

병사수: 1 생존자: 1 
병사수: 2 생존자: 2 
병사수: 3 생존자: 2 
병사수: 4 생존자: 1 
병사수: 5 생존자: 4 
병사수: 6 생존자: 1 
병사수: 7 생존자: 4 
병사수: 8 생존자: 7 
병사수: 9 생존자: 1 
병사수: 10 생존자: 4 
병사수: 11 생존자: 7 
병사수: 12 생존자: 10 
병사수: 13 생존자: 13 
병사수: 14 생존자: 2 
병사수: 15 생존자: 5 
병사수: 16 생존자: 8 
병사수: 17 생존자: 11 
병사수: 18 생존자: 14 
병사수: 19 생존자: 17 
병사수: 20 생존자: 20 
병사수: 21 생존자: 2 
병사수: 22 생존자: 5 
병사수: 23 생존자: 8 
병사수: 24 생존자: 11 
병사수: 25 생존자: 14 
병사수: 26 생존자: 17 
병사수: 27 생존자: 20 
병사수: 28 생존자: 23 
병사수: 29 생존자: 26 
병사수: 30 생존자: 29 
병사수: 31 생존자: 1 
병사수: 32 생존자: 4 
병사수: 33 생존자: 7 
병사수: 34 생존자: 10 
병사수: 35 생존자: 13 
병사수: 36 생존자: 16 
병사수: 37 생존자: 19 
병사수: 38 생존자: 22 
병사수: 39 생존자: 25 
병사수: 40 생존자: 28 
병사수: 41 생존자: 31