데이터 과학을 위한 R 알고리즘

유클리드 호제법(Euclidean Algorithm)-최대공약수

1. 타일 문제 정의 ¹

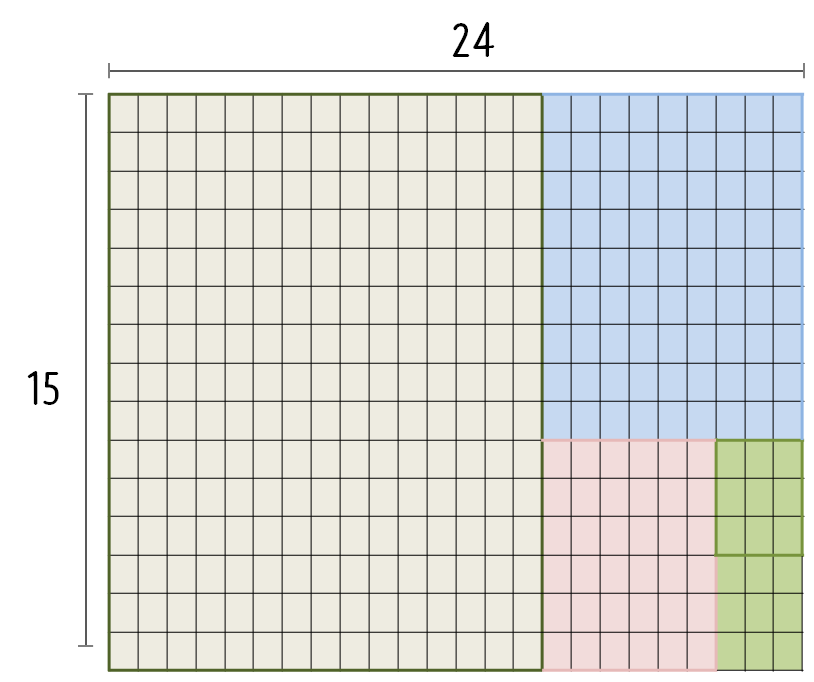
직사각형 모향으로 된 바닥이 있는데, 바닥크기가 \(15 \times 24\) 를 갖고 있다. 타일을 깔아야 하는데, 바닥을 빈공간 없이 모두 채울 수 있는 최대 크기 타일 크기를 계산해 보자. 최대공약수를 찾아가는 과정은 \(15 \times 24\) → \(15 \times 15\) → \(9 \times 9\) → \(3 \times 3\) 으로 찾아가게 되어 결국, \(3 \times 3\) 크기 타일을 $8 = 40 $ 장 붙이면 바닥이 꽉 차게 된다.

2. 최대공약수 컴퓨터

gmp 팩키지 factorize() 함수를 사용하면 자연수에 대한 인수분해를 수행할 수 있다. 이를 통해 두 자연수 사이 최대 공약수를 찾아낼 수 있다. 즉, 24를 소인수 분해하면 \(24 = 2 \times 2 \times 2 \times 3\)가 되고, 15는 \(15 = 3 \times 5\)가 되어 두 자연수 사이 최대 공약수는 3 이 된다.

# 1. 최대공약수 ------------------
gmp::factorize(24)

Error in loadNamespace(name): there is no package called 'gmp'

gmp::factorize(15)

Error in loadNamespace(name): there is no package called 'gmp'

3. 최대공약수 손으로 계산하기

두 자연수 사이 최대공약수를 유클리드 알고리즘으로 다음 과정을 거쳐 계산한다.

1. 두자연 24 와 15를 비교한다.
2. 24가 크기 때문에 24를 15로 나눈다.
   • 24를 15로 나누게 되면 항상 두가지가 성립한다.
   • 24는 15보다 항상 크고, 15는 나머지 9보다 항상 크다.
3. 다시 15를 9로 나눈다.
4. 이런 과정을 반복하여 나머지가 0이 될때까지 반복한다.

\[\begin{align} 24 &= 15 \times 1 + 9 \\ 15 &= 9 \times 1 + 6 \\ 9 &= 6 \times 1 + 3 \\ 6 &= 3 \times 2 + 0 \end{align}\]

4. 유클리드 알고리즘 ²

유클리드 알고리즘을 프로그래밍 언어로 구현하는 방식은 while 루프를 이용하는 방법과 재귀를 이용하는 방법으로 구현을 해보자.

4.1. while 루프 활용

첫번째 자연수 숫자 (\(D\))가 있고,

\[D = \text{number_a} \times \text{number_b} + \text{나머지}\]

상기 재귀식을 활용하여 첫번째 숫자(\(\text{number_a}\))를 두번째 숫자(\(\text{number_b}\))로 나누기를 반복하는데, \(\text{number_a}==0\)이 되면 while 루프를 빠져나온다. 그리고 나서 마지막 \(\text{number_a}\)을 반환한다.

gcd_while <- function(number_a, number_b)
{

  while(number_b != 0) {
    remainder <- number_a %% number_b
    number_a  <- number_b
    number_b  <- remainder
  }
  return(number_a)
}

gcd_while(24, 15) # 3

[1] 3

gcd_while(54, 24) # 6

[1] 6

4.2. 재귀 활용

while 루프로 코딩된 것을 재귀 코드로 바꿔 구현할 수도 있다. ³

## 2.2. 재귀를 활용한 방법 --------------

gcd_recursion <- function(number_a, number_b) {
  
  remainder <- number_a %% number_b
  return(ifelse(remainder, gcd_recursion(number_b, remainder), number_b))
}

gcd_recursion(24, 15) # 3
gcd_recursion(54, 24) # 6
``