데이터 과학을 위한 R 알고리즘
이진검색(Binary Search)
1. 이진 검색
이진검색은 데이터가 벡터로 저장되어 있다고 가정할 때, 해당 값이 어느 위치에 있는지 찾아내는 알고리즘이다.
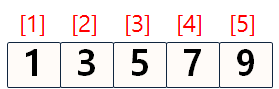
- 이진검색은 단순 검색보다 훨씬 빠르다.
- \(\mathcal{O}(log(n))\)은 \(\mathcal{O}(n)\) 보다 훨씬 빠른데, 특히 찾고자 하는 항목이 늘어날수록 확실한 속도차이를 체감한다.
- 알고리즘 시간은 빅오(\(\mathcal{O}\)) 표기법으로 작성되고, 시분초가 아닌 알고리즘 성장으로 측정한다.
1.1. 반복을 활용한 이진 검색
로제타코드 - Binary search의 알고리즘을 기초로 이진검색을 binary_search 함수로 구현하면 다음과 같다. 찾고자 하는 항목(item)을 벡터로 넣어 두고, 벡터의 중간값과 항목을 비교하여 최종적으로 벡터의 중간값과 항목이 같은 경우 몇번째 위치했는지 인덱스를 반환한다. R은 벡터 인덱스가 0이 아니라 1부터 시작된다.
# 반복을 활용한 이진검색 함수
binary_search <- function(vec, item) {
low <- 1L
high <- length(vec)
while(low <= high) {
mid <- floor((low + high) /2L)
if(vec[mid] == item) {
return(mid)
} else if(item < vec[mid]) {
high <- mid -1
} else {
low <- mid +1
}
}
return(NULL)
}
# 이진 검색 실행
vec <- c(1,3,5,7,9)
binary_search(vec, 7) ## [1] 4binary_search(vec, -1)## NULL1.2. 반복을 활용한 이진 검색 파이썬 코드
2. 선형검색
선형검색은 순차적으로 벡터로 저장된 저장공간을 하나씩 비교하면서 찾아가는 방식이다. 따라서 찾고자 하는 항목(item)이 가장 마지막에 위치한 경우 가장 많은 시간이 소요된다. 반면에 첫번째 위치한 경우 시간이 가장 적게 소요된다.
linear_search <- function(vec, item) {
high <- length(vec)
for (i in 1:high) {
if (vec[i] == item) {
return(i)
}
}
return(NULL)
}
vec <- c(1,3,5,7,9)
linear_search(vec, 9)## [1] 5linear_search(vec, 6)## NULL2.1. 선형검색과 이진검색 비교
선형검색과 이진검색을 비교하여 소요된 시간을 비교하면 다음과 같다.
| 선형검색 | 이진검색 |
|---|---|
| 100개 항목 → 100번 검색 | 100개 항목 → 7번 검색(log2(100)=6.6) |
| 7,000,000,000개 항목 → 7,000,000,000번 검색 | 7,000,000,000개 항목 → 33번 검색(log2(7,000,000,000) = 32.7) |
| \(\mathcal{O}(n)\) | \(\mathcal{O}(log(n))\) |
