xwMOOC 데이터 과학
멀티코어 병렬 프로그래밍 - doParallel
1. 회문 (Palindrome) 1
문자에 대한 회문은 도처에서 많이 찾을 수 있다. 숫자에 대한 회문을 바탕으로 멀티코어를 활용하여 병렬프로그램을 작성하는 방법을 살펴본다.
get_digit 함수를 통해 입력받은 숫자의 n번째 자리수 숫자를 뽑아내는 함수를 작성하고 이를 바탕으로 회문 숫자인지를 palindrome 함수로 판별한다. 그리고 숫자 자리수에 맞춰 첫째자리, 둘째자리, … 순으로 두 숫자를 곱해서 나온 숫자 중 가장 큰 회문 숫자를 biggest_palindrome 함수를 통해 찾아보자.
# 0. 환경설정 --------
# library(doParallel)
# library(tidyverse)
# 1. 기본함수 -------
## 1.1. 숫자의 n번째 자리수 숫자를 뽑아내는 함수
get_digit <- function(num, n) {
# 왼쪽부터 숫자의 자리수를 제거하고 나서, 오른쪽 자리수 숫자를 제거
(num %% (10 ^ n)) %/% (10 ^ (n-1))
}
## 1.2. 양의 정수가 회문인지 판정하는 함수
palindrome <- function(num) {
digits <- floor(log(num, 10)) + 1
for (x in 1:((digits %/% 2))) {
digit1 <- get_digit(num, x)
digit2 <- get_digit(num, (digits + 1) - x)
if (digit1 != digit2)
return(FALSE)
}
return(TRUE)
}
## 1.3. 세자리, 네자리, 다섯자리 ... 등등 가장 큰 회문 숫자를 탐색
biggest_palindrome <- function(digits=3) {
min_digit <- 10^(digits-1)
max_digit <- 10^digits -1
best <- 0
for (x in min_digit:max_digit) {
for (y in x:max_digit) {
candidate <- x * y
if (candidate > best && palindrome(candidate)) {
best <- candidate
}
}
}
return(best)
}상기 함수를 통해 순차적으로 계산된 결과는 다음과 같다.
- 십자리:
biggest_palindrome(1)를 실행하면 9. - 백자리:
biggest_palindrome(2)를 실행하면 9009. - 천자리:
biggest_palindrome(3)를 실행하면 906609. - 만자리:
biggest_palindrome(4)를 실행하면 99000099.
2. 병렬처리 2
순차 컴퓨팅은 문제를 일련의 이산 명령어 집합으로 나눠서 순차적으로 단일 CPU 프로세서로 처리하는 반면에, 병렬 컴퓨팅은 문제를 몇개에서 수십개의 CPU 프로세서(코어)로 나누어서 처리 가능한 형태로 변형한 후에 병렬적으로 처리한다.
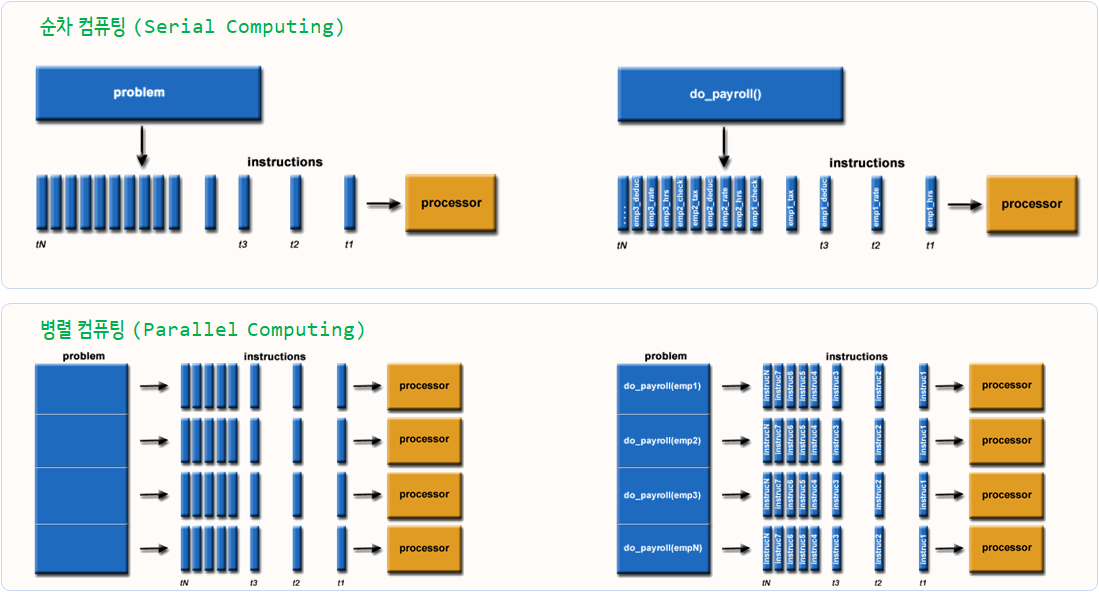
플린 분류(영어: Flynn taxonomy)는 마이클 플린이 1966년에 제안한 컴퓨터 아키텍처 분류로, 일반인이 쉽게 이해하는 방식으로 보면 처리할 데이터와 처리할 CPU 프로세서에 따라 다음과 같이 네가지로 구분한다.
- SISD(Single Instruction, Single Data stream)
- SIMD(Single Instruction, Multiple Data streams)
- MISD(Multiple Instruction, Single Data stream)
- MIMD (Multiple Instruction, Multiple Data streams)
2.1. for 구문
가장 먼저 for문을 통해 총 소요시간을 구해본다.
# 2. 순차처리부터 병렬처리 -------
## 2.1. 순차처리 -----
elapsed_for_v <- numeric(4)
for(i in 1:4) {
elapsed_for_v[i] <- system.time(biggest_palindrome(i))[3]
}
elapsed_for_v[1] 0.00 0.02 0.16 4.42
2.2. for 구문
foreach를 통해 순차적인 병렬처리를 수행해본다.
## 2.2. 순차처리 foreach -----
elapsed_foreach_v <- numeric(4)
foreach(i = 1:4) %do% {
elapsed_foreach_v[i] <- system.time(biggest_palindrome(i))[3]
}[[1]]
elapsed
0
[[2]]
elapsed
0
[[3]]
elapsed
0.17
[[4]]
elapsed
4.58
elapsed_foreach_v[1] 0.00 0.00 0.17 4.58
2.3. foreach 병렬 구문
최근 컴퓨터를 구입하게 되면 대부분 멀티코어가 들어있는 하드웨어를 갖고 있다. 따라서, 병렬처리를 위해서는 makeCluster를 통해 코어로 구성된 클러스터를 구성하고 나서 이를 병렬처리를 수행한다.
## 2.3. 병렬처리 foreach -----
cl <- makeCluster(detectCores())
registerDoParallel(cl)
elapsed_parallel_v <-
system.time (
palindrome_df <- foreach(i=1:4, .combine='rbind.data.frame',
.multicombine=TRUE,
.export=c("get_digit","palindrome")) %dopar% {
biggest_palindrome(i)
}
) [3]
stopCluster(cl)
elapsed_parallel_velapsed
33
2.4. 결과 비교
자리수가 4자리가 되면 제법 소요시간이 소요된다. 5자리가 되면 유의민한 숫자가 될 것이지만 너무 큰 숫자라 더이상 회문 숫자를 구할 수가 없다. 그리고, 단일 코어에서 계산되면 빠를 것을 코어 다수에서 나눠 계산을 하게 되어 전체적인 시간이 더 늘어났다.
병렬처리작업을 수행할 경우 문제를 병렬처리가 가능한 형태로 나눠 각 코어에 분배하여 처리할 경우 원하는 효과를 거둘 수 있다.
# 3. 분석결과 정리 -----
data.frame("for루프" = elapsed_for_v, "foreach"=elapsed_foreach_v) %>%
mutate(병렬=elapsed_parallel_v,
자리수=c(10,100,1000,10000)) %>%
select(자리수, everything()) %>%
DT::datatable()Error: <text>:5:10: unexpected '<'
4: data.frame("for<U+B8E8><U+D504>" = elapsed_for_v, "foreach"=elapsed_foreach_v) %>%
5: mutate(<
^
