피보나치 수(Fibonacci Number)
학습 목표
- 피보나치 수를 통해 수학을 이해한다는 의미를 되새긴다.
- 피보나치 수를 수치적, 대수적, 기하적, 실생활에 대해서 살펴본다.
- 피보나치 수를 파이썬/R 코드로 코딩한다.
1. 피보나치 수
레오나르도 피보나치(Leonardo Fibonacci, 1170년~1250년)는 일찍이 아버님을 따라 어린 나이에 북아프리카에서 아라비아 상인과 교역을 통해 당시 유럽에서는 사용되지 않던 고급 수학을 경험하고 이를 이탈리아로 돌아가서 피보나치 수를 비롯한 수학을 잘 정리해서 유럽에 소개했다. 물론 피보나치가 처음 이 수열을 발견한 것은 아니다.
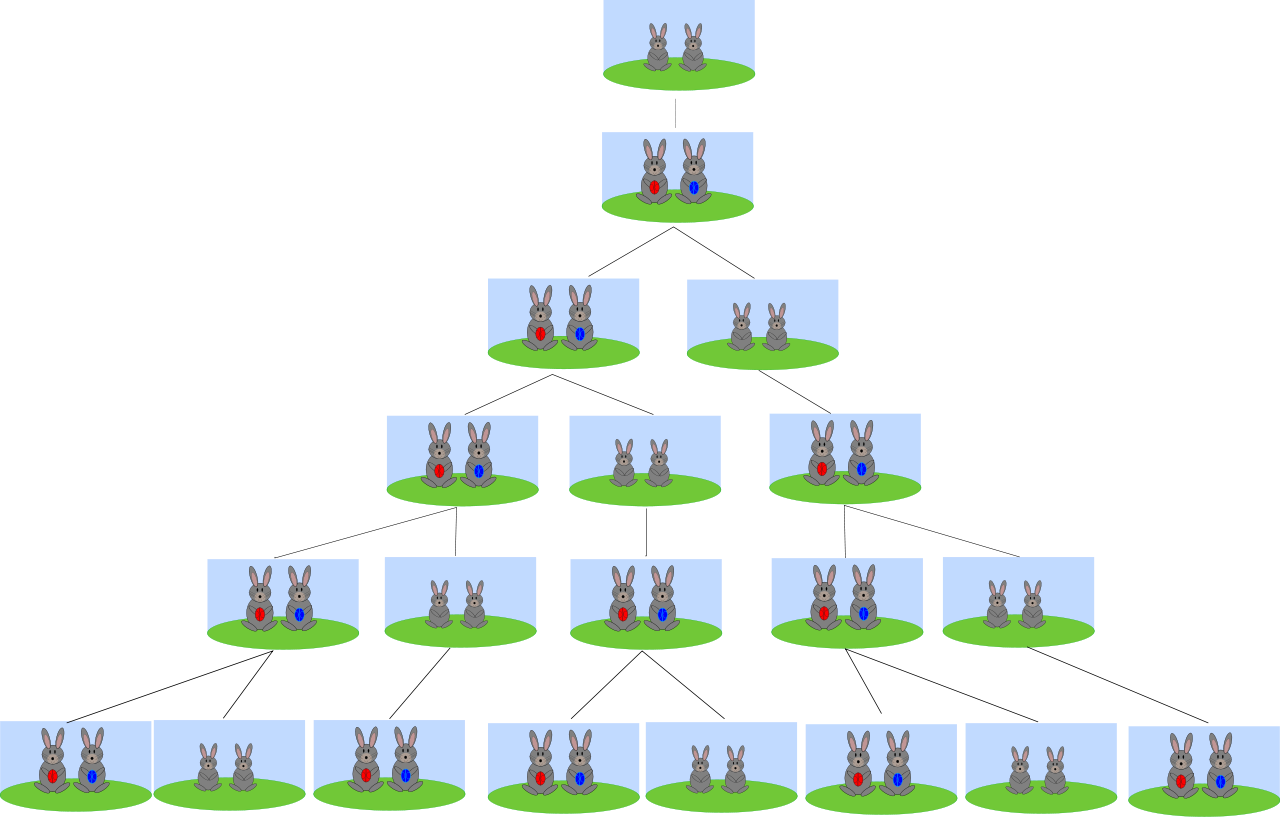
2. 수치로 이해하는 피보나치 수
토끼가 1월에 한쌍이 있고, 성인 토끼로 자라는데 한달이 필요하고, 한달에 한쌍 토끼를 낳고, 절대로 죽지 않는다고 가정한다. 그렇면 1202년 출간된 피보나치 토끼 퀴즈가 완성된다.
| 시간 | 1월 | 2월 | 3월 | 4월 | 5월 | 6월 | 7월 | 8월 | 9월 | 10월 | 11월 | 12월 | 1월 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 미성년 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 |
| 성년 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 |
| 총합 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 |
마지막, 총합, \(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, \cdots\) 순열을 피보나치 순열이라고 부른다.
3. 대수로 이해하는 피보나치 수 1
수치로 표현된 순열을 기호로 표현해 보면 다음과 같다.
\[F_n = F_{n-1} + F_{n-2}\]
초기값으로 \(F_1 = 1,\; F_2 = 1\) 혹은, \(F_0 = 0,\; F_1 = 1\) 을 사용한다.
4. 기하로 이해하는 피보나치 수 2
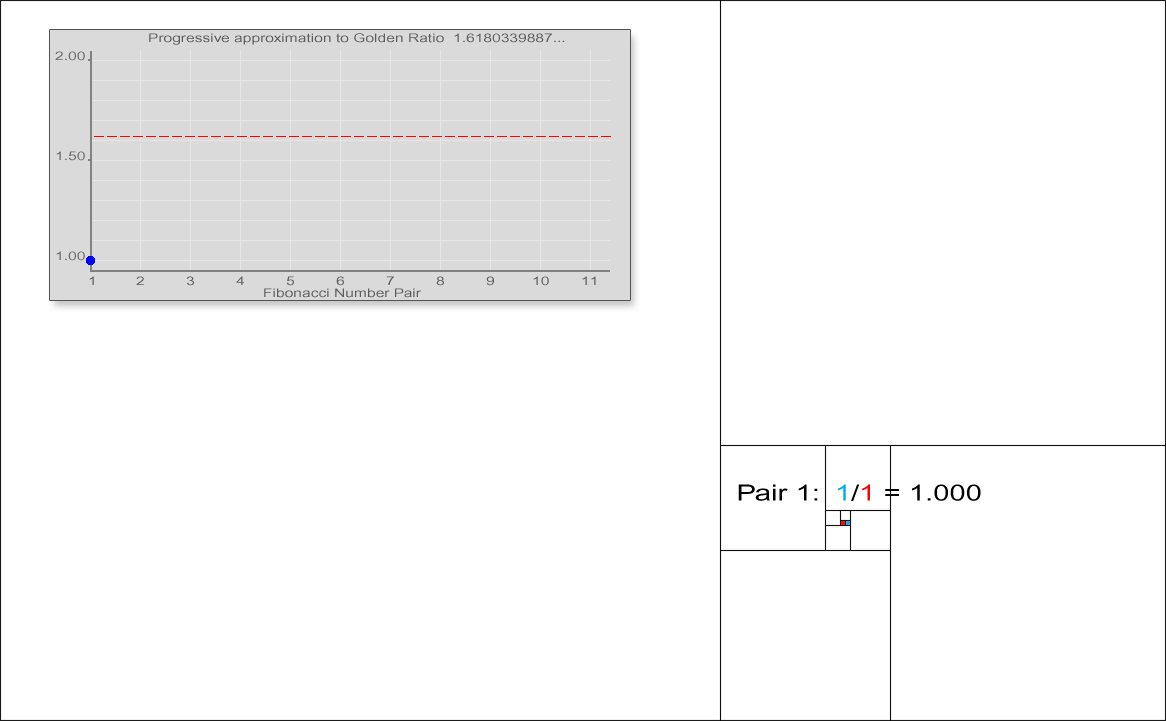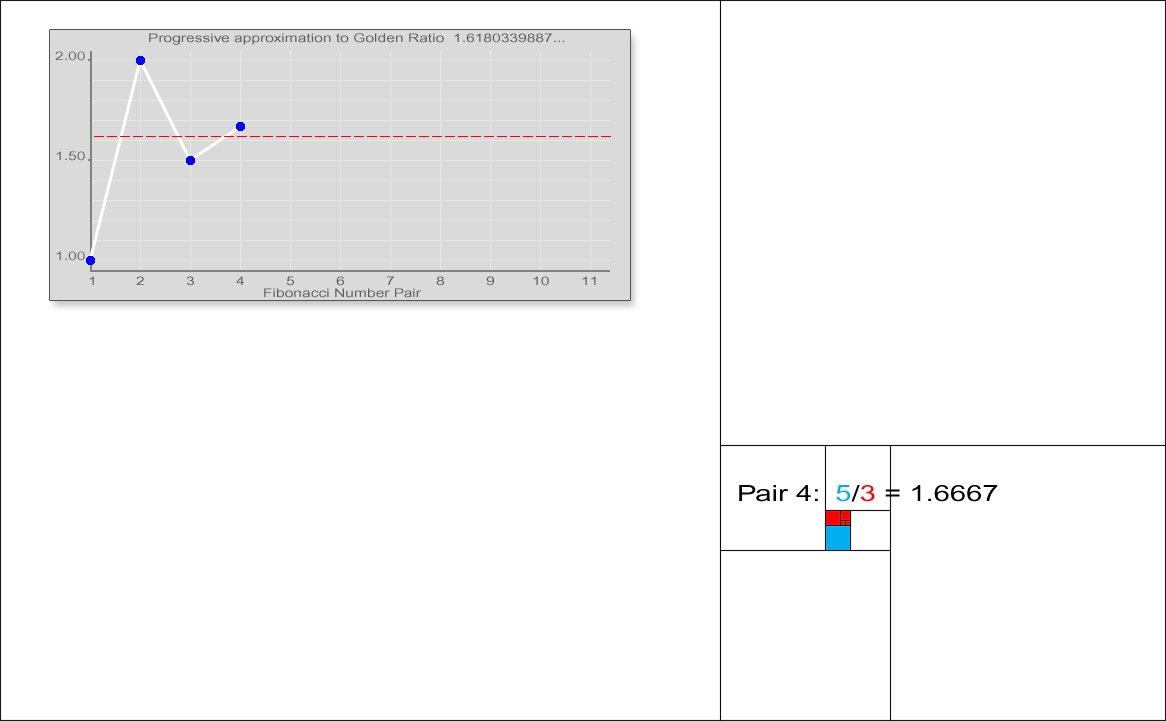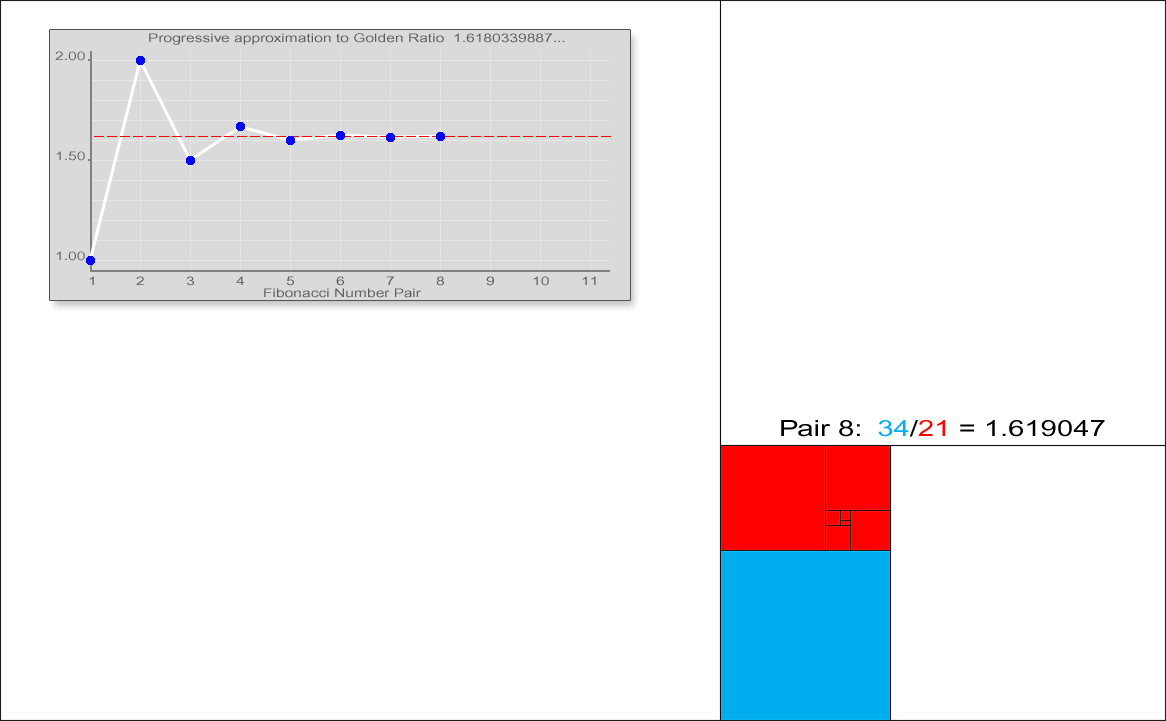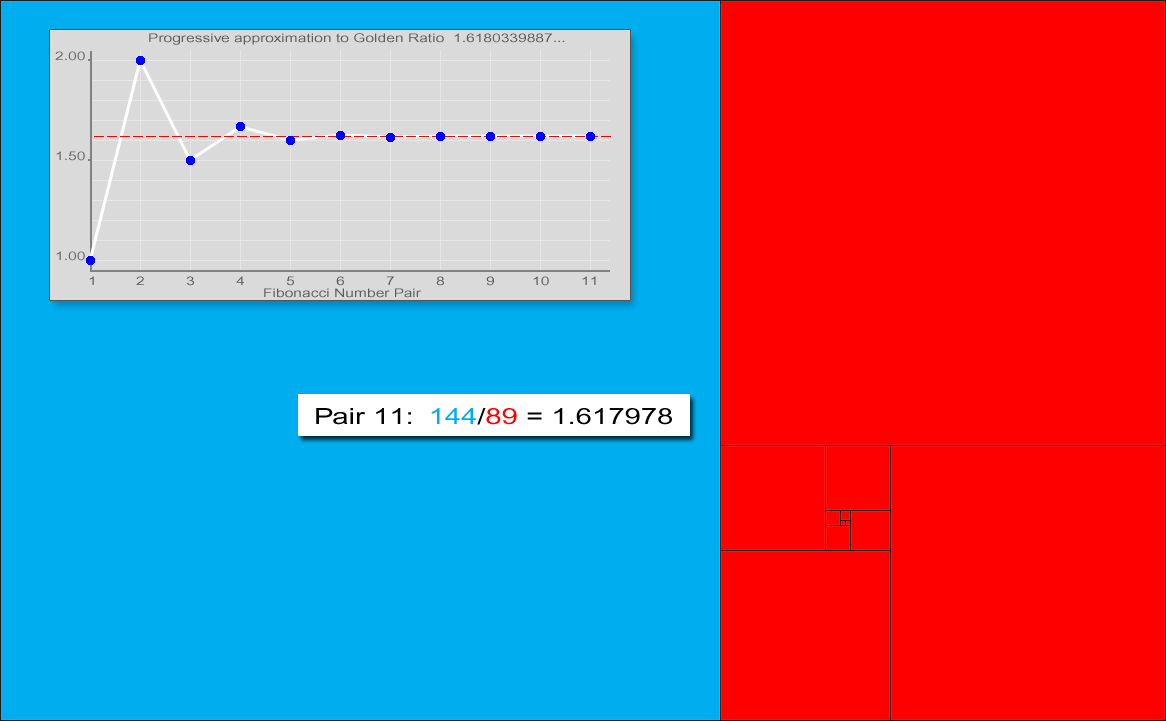
피보나치 수열은 황금비(Golden Ratio)와 관련이 있는데, 인접한 두항의 비 \(\frac{F_{n+1}}{F_n}\)는 황금비(\(1:1.6180339887\cdots\))에 수렴한다.
즉, \(\lim_{n\to\infty} = \frac{F_{n+1}}{F_n} = \Phi\), \(0,1,1,2,3,5,8,13,21,34,55,89,144,233\cdots\).
- \(\frac{3}{2} = 1.5\)
- \(\frac{5}{3} = 1.6666 66667\)
- \(\frac{8}{5} = 1.6\)
- \(\frac{13}{8} = 1.625\)
- \(\frac{21}{13} = 1.61538 46154...\)
- \(\frac{34}{21} = 1.61904 719\)
- \(\frac{55}{34} = 1.61764 70588...\)
- \(\frac{89}{55} = 1.61818 18182...\)
- \(\frac{144}{89} =1.61797 75281...\)
- \(\frac{233}{144} = 1.61805 55556...\)
4.1. 황금비(Golden Ratio)

황금비는 \(\frac {x}{y} = \frac{x+y}{x}\)를 만족한다. 황금비를 \(\Phi=\frac{x}{y}\)로 두고 수식을 정리하면 다음과 같다.
\[\Phi = 1 + \frac{1}{\Phi}\]
수식을 풀면
\[\Phi = \frac{\sqrt{5}+1}{2} \approx 1.618 \]
5. 프로그래밍 코드 3
피보나치 순열을 코드로 작성하는 방법은 다음과 같다.
- 수치해석(Analytic)
- 반복(Iterative)
- 재귀(Recursive)
- 메모이제이션 재귀(Recursive with Memoization)
yield를 사용한 Generative
def fib(n):
if n < 2:
return n
else:
return fib(n-1) + fib(n-2)1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040물론 R로도 가능하다. 재귀 방식으로 피보나치 순열을 뽑아내는 R 코드가 다음에 나타나 있다.
# 재귀방식 구현
recfibo <- function(n) {
if ( n < 2 ) n
else Recall(n-1) + Recall(n-2)
}
# 첫 21개 숫자 출력
print.table(lapply(0:20, recfibo)) [1] 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765