재현가능한 과학적 분석을 위한 R

벡터화

학습 목표

R에 나오는 벡터화 연산 이해한다.

R 함수 대부분은 벡터화되었다. 즉, 한번에 각 요소에 대해 연산을 수행하도록 루프를 돌릴 필요없이 함수가 벡터 모든 요소에 대해 연산작업을 수행한다. 이렇게 되면 코드는 더욱 간결해지고, 가독성이 높아지고, 오류에 덜 노출된다.

x <- 1:4
x * 2

[1] 2 4 6 8

곱하기는 벡터 모든 요소에 일어난다.

벡터를 두개 더할 수도 있다:

y <- 6:9
x + y

[1]  7  9 11 13

x 벡터 각 요소가 y 벡터 대응되는 요소에 더해진다:

x:  1  2  3  4
    +  +  +  +
y:  6  7  8  9
---------------
    7  9 11 13

도전과제 1

gapminder 데이터셋 pop 칼럼에 벡터 연산을 시도해 본다.

gapminder 데이터프레임에 신규 칼럼을 생성하는데, 백만명 단위로 인구정보를 표현한다. 데이터프레임에 head 혹은 tail 명령어를 적용해서 실제로 제대로 동작하는지 확인한다.

도전과제 2

그래프 하나에, 모든 국가에 대해 백만 단위로 인구를 연도별로 도식화한다. 어느 국가인지 식별하는 것은 신경쓰지 않는다.

상기 연습문제를 반복하면서, 중국(China), 인도(India), 인니(Indonesia)에 대해서만 도식화한다. 마찬가지로, 어는 국가인지 식별하는 것은 신경쓰지 않는다.

비교 연산자, 논리 연산자, 그리고 많은 함수도 벡터화를 지원한다:

비교 연산자

x > 2

[1] FALSE FALSE  TRUE  TRUE

논리 연산자

a <- x > 3  # 혹은 명확하게, a <- (x > 3)
a

[1] FALSE FALSE FALSE  TRUE

함수 대부분은 또한 벡터에 요소별(element-wise)로 연산작업을 수행한다:

Functions

x <- 1:4
log(x)

[1] 0.0000000 0.6931472 1.0986123 1.3862944

벡터화 연산은 행렬에 요소별로 연산작업을 수행한다:

m <- matrix(1:12, nrow=3, ncol=4)
m * -1

     [,1] [,2] [,3] [,4]
[1,]   -1   -4   -7  -10
[2,]   -2   -5   -8  -11
[3,]   -3   -6   -9  -12

Tip: 요소별(element-wise) 곱셈 vs. 행렬 곱셈

매우 중요: * 곱하기 연산은 요소별 곱셈 결과를 전달한다! 행렬 곱셈을 하려면, %*% 연산자를 사용한다:

m %*% matrix(1, nrow=4, ncol=1)

     [,1]
[1,]   22
[2,]   26
[3,]   30

matrix(1:4, nrow=1) %*% matrix(1:4, ncol=1)

     [,1]
[1,]   30

행렬 대수에 관한 더 많은 정보는 Quick-R reference guide을 참조한다.

도전과제 3

다음과 같은 행렬이 주어졌다:

m <- matrix(1:12, nrow=3, ncol=4)
m

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

다음 명령어를 실행하면, 연산작업 결과가 어떻게 될지 생각한 것을 적어본다:

m ^ -1
m * c(1, 0, -1)
m > c(0, 20)
m * c(1, 0, -1, 2)

예상한 출력결과가 나왔나요? 만약 그렇지 않다면, 도우미를 부르세요!

도전과제 4

다음 연속된 분수 합계를 구하는데 관심이 있다:

 x = 1/(1^2) + 1/(2^2) + 1/(3^2) + ... + 1/(n^2)

이 모두를 타이핑하는 것은 지루하고, n 값이 매우 큰 경우 불가능하다. 벡터화를 사용해서 n=100 일 때 x를 계산한다. n=10,000 일 때, 합은 얼마나 될까?

도전과제 해답

도전과제 1 에 대한 해답

gapminder 데이터셋 pop 칼럼에 벡터 연산을 시도해 본다.

gapminder$pop_millions <- gapminder$pop / 1e6
head(gapminder)

      country year      pop continent lifeExp gdpPercap pop_millions
1 Afghanistan 1952  8425333      Asia  28.801  779.4453     8.425333
2 Afghanistan 1957  9240934      Asia  30.332  820.8530     9.240934
3 Afghanistan 1962 10267083      Asia  31.997  853.1007    10.267083
4 Afghanistan 1967 11537966      Asia  34.020  836.1971    11.537966
5 Afghanistan 1972 13079460      Asia  36.088  739.9811    13.079460
6 Afghanistan 1977 14880372      Asia  38.438  786.1134    14.880372

도전과제 2 에 대한 해답

백만단위 인구를 연도에 대해 도식화해서 도식화 기술을 상기한다.

plot(gapminder$year, gapminder$pop_millions)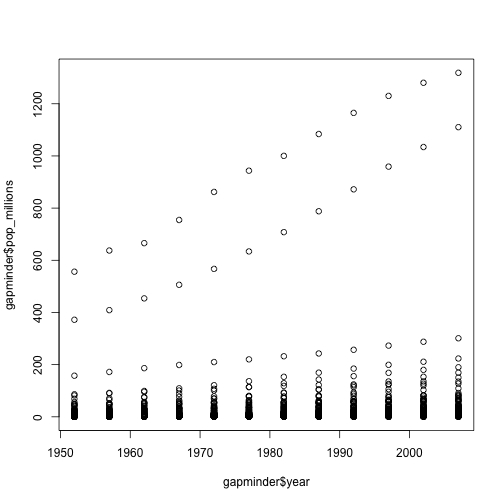

plot of chunk ch2-sol

countryset <- c('China', 'India', 'Indonesia')
y <- gapminder[gapminder$country %in% countryset, ]
plot(y$year, y$pop_millions)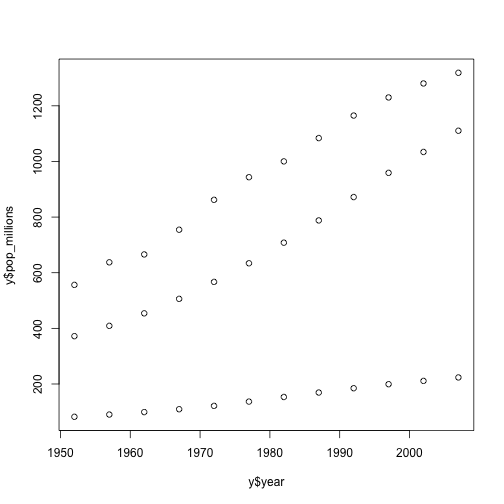

plot of chunk ch2-sol

도전과제 3 에 대한 해답

다음과 같은 행렬이 주어졌다:

m <- matrix(1:12, nrow=3, ncol=4)
m

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

다음 명령어를 실행하면, 연산작업 결과가 어떻게 될지 생각한 것을 적어본다:

m ^ -1

          [,1]      [,2]      [,3]       [,4]
[1,] 1.0000000 0.2500000 0.1428571 0.10000000
[2,] 0.5000000 0.2000000 0.1250000 0.09090909
[3,] 0.3333333 0.1666667 0.1111111 0.08333333

m * c(1, 0, -1)

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    0    0    0    0
[3,]   -3   -6   -9  -12

m > c(0, 20)

      [,1]  [,2]  [,3]  [,4]
[1,]  TRUE FALSE  TRUE FALSE
[2,] FALSE  TRUE FALSE  TRUE
[3,]  TRUE FALSE  TRUE FALSE

m * c(1, 0, -1, 2)

     [,1] [,2] [,3] [,4]
[1,]    1    8   -7    0
[2,]    0    5   16  -11
[3,]   -3    0    9   24

도전과제 4 에 대한 해답

다음 연속된 분수 합계를 구하는데 관심이 있다:

 x = 1/(1^2) + 1/(2^2) + 1/(3^2) + ... + 1/(n^2)

sum(1/(1:100)^2)

[1] 1.634984

sum(1/(1:1e04)^2)

[1] 1.644834

n <- 10000
sum(1/(1:n)^2)

[1] 1.644834

함수를 사용해서 동일한 결과를 얻을 수도 있다:

inverse_sum_of_squares <- function(n) {
  sum(1/(1:n)^2)
}
inverse_sum_of_squares(100)

[1] 1.634984

inverse_sum_of_squares(10000)

[1] 1.644834

n <- 10000
inverse_sum_of_squares(n)

[1] 1.644834