xwMOOC 기계학습

통계적 모형개발 기초

1. 통계 모형 개발과정

통계모형 개발과정은 데이터 과학 프로세스에서 크게 차이가 나지 않는다. 다만, 일반적인 통계모형을 개발할 경우 다음과 같은 과정을 거치게 되고, 지난한 과정이 될 수도 있다.

1. 데이터를 정제하고, 모형에 적합한 데이터(R과 모형 팩키지와 소통이 될 수 있는 데이터형태)가 되도록 준비한다.
2. 변수에 대한 분포를 분석하고 기울어짐이 심한 경우 변수변환도 적용한다.
3. 변수와 변수간에, 종속변수와 설명변수간에 산점도와 상관계수를 계산한다. 특히 변수간 상관관계가 \(r > 0.9\) 혹은 근처인 경우 변수를 빼거나 다른 방법을 강구한다.
4. 동일한 척도로 회귀계수를 추정하고 평가하려는 경우, scale() 함수로 척도로 표준화한다.
5. 모형을 적합시킨 후에 잔차를 보고, 백색잡음(whitenoise)인지 확인한다. 만약, 잔차에 특정한 패턴이 보이는 경우 패턴을 잡아내는 모형을 새로 개발한다.
   1. plot() 함수를 사용해서 이상점이 있는지, 비선형관계를 잘 잡아냈는지 시각적으로 확인한다.
   2. 다양한 모형을 적합시키고 R^2 와 RMSE, 정확도 등 모형평가 결과가 가장 좋은 것을 선정한다.
   3. 절약성의 원리(principle of parsimony)를 필히 준수하여 가장 간결한 모형이 되도록 노력한다.
6. 최종 모형을 선택하고 모형에 대한 해석결과와 더불어 신뢰구간 정보를 넣어 마무리한다.

2. 과대적합 사례

\(y=x^2 + \epsilon\) 오차는 정규분포 평균 0, 표준편차 0.2를 갖는 모형을 따른다고 가정하고, 이를 차수가 높은 다항식을 사용하여 적합시킨 결과를 확인하는 절차는 다음과 같다.

1. tidyr, modelr, ggplot2 팩키지를 불러와서 환경을 설정한다.
2. \(y=x^2 + \epsilon\), 오차는 \(N(0, 0.25)\)을 따르는 모형을 생성하고, df 데이터프레임에 결과를 저장한다.
3. poly_fit_model 함수를 통해 7차 다항식으로 적합시킨다.
4. 적합결과를 ggplot을 통해 시각화한다.

#--------------------------------------------------------------------------------
# 01. 환경설정
#--------------------------------------------------------------------------------
library(tidyr)
library(modelr)
library(ggplot2)
#--------------------------------------------------------------------------------
# 02. 참모형 데이터 생성: y = x**2
#--------------------------------------------------------------------------------

true_model <- function(x) {
  y = x ** 2 + rnorm(length(x), sd=0.25)
  return(y)
}

x = seq(-1,1, length=20)
y = true_model(x)
df <- data.frame(x,y)

#--------------------------------------------------------------------------------
# 03. 10차 다항식 적합
#--------------------------------------------------------------------------------

poly_fit_model <- function(df, order) {
  lm(y ~ poly(x, order), data=df)
}

fitted_mod <- poly_fit_model(df, 7)

#--------------------------------------------------------------------------------
# 04. 적합결과 시각화
#--------------------------------------------------------------------------------

grid <- df %>% tidyr::expand(x = seq_range(x, 50))
preds <- grid %>% modelr::add_predictions(fitted_mod, var = "y")

df %>% 
  ggplot(aes(x, y)) +
  geom_line(data=preds) +
  geom_point()

modelr::rmse(fitted_mod, df)

[1] 0.1893603

3. 전통적인 가내수공업 방식 모형개발 사례

데이터과학 제품을 만드는 방식은 여러가지 방식이 존재한다. 공학적인 방식으로 보면 장인이 제자에게 비법을 가미해서 전통적으로 내려오던 가내수공업 방식부터 컨베이어 벨트를 타고 포드생산방식을 거쳐 Mass Customization을 지나 기계학습과 딥러닝이 결합된 모형개발 방식까지 정말 다양한 방식이 혼재되어 있다.

전통적인 가내수공업 방식은 인간이 가장 많은 것을 이해하고 주문형 모형을 만들어내는 가장 최적의 방식이다. 이를 간략하게 살펴본다.

##========================================================
## 01. 데이터 준비
##========================================================
## 모의시험 데이터 생성

x <- seq(1, 100,1)
y <- x**2 + jitter(x, 1000)

df <- data.frame(x,y)
head(df)

  x          y
1 1  136.72375
2 2  -50.86586
3 3 -169.66308
4 4   96.48862
5 5   67.82954
6 6  -94.61818

##========================================================
## 02. 탐색적 데이터 분석
##========================================================
# 통계량
psych::describe(df)

  vars   n    mean      sd  median trimmed     mad     min      max
x    1 100   50.50   29.01   50.50   50.50   37.06    1.00   100.00
y    2 100 3429.21 3070.14 2511.15 3127.73 3232.05 -169.66 10093.96
     range skew kurtosis     se
x    99.00 0.00    -1.24   2.90
y 10263.62 0.62    -0.88 307.01

# 산점도
plot(x, y)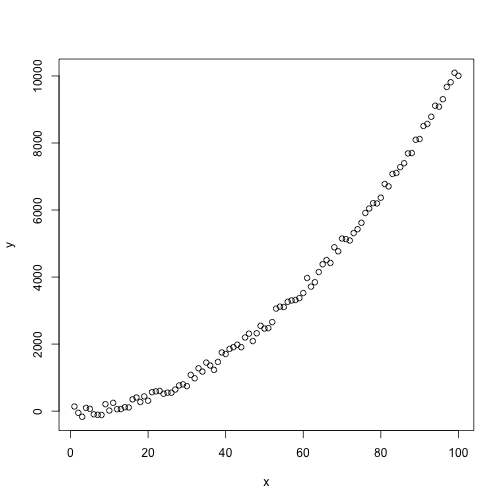

##========================================================
## 03. 모형 적합
##========================================================

#---------------------------------------------------------
# 3.1. 선형회귀 적합
lm.m <- lm(y ~ x, data=df)
summary(lm.m)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-1003.8  -632.5  -272.4   487.7  1783.3 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1749.127    153.699  -11.38   <2e-16 ***
x             102.541      2.642   38.81   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 762.7 on 98 degrees of freedom
Multiple R-squared:  0.9389,    Adjusted R-squared:  0.9383 
F-statistic:  1506 on 1 and 98 DF,  p-value: < 2.2e-16

par(mfrow=c(1,2))
# 적합모형 시각화
plot(x,y, data=df, cex=0.7)
abline(lm.m, col='blue')

# 잔차 
plot(resid(lm.m))
abline(h=0, type='3', col='blue')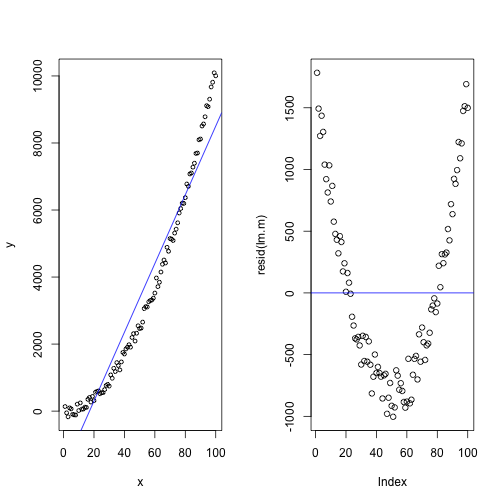

#---------------------------------------------------------
# 3.2. 비선형회귀 적합
# 비선형회귀적합
df$x2 <- df$x**2

nlm.m <- lm(y ~ x + x2, data=df)
summary(nlm.m)

Call:
lm(formula = y ~ x + x2, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-192.576  -96.514   -9.126  102.801  202.867 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -29.52909   35.67210  -0.828    0.410    
x             1.38848    1.63031   0.852    0.396    
x2            1.00151    0.01564  64.040   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 116.5 on 97 degrees of freedom
Multiple R-squared:  0.9986,    Adjusted R-squared:  0.9986 
F-statistic: 3.431e+04 on 2 and 97 DF,  p-value: < 2.2e-16

par(mfrow=c(1,2))
# 적합모형 시각화
plot(x, y, data=df, cex=0.7)
lines(x, fitted(nlm.m), col='blue')
# 잔차 
plot(resid(nlm.m), cex=0.7)
abline(h=0, type='3', col='blue')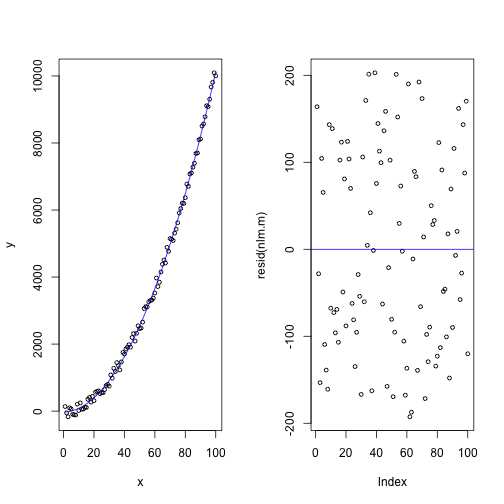

데이터를 준비하고 \(y = \beta_0 + \beta_1 x + \beta_1 x^2\) 수식으로 돌아가는 시스템에서 데이터를 추출하고 이를 먼저 선형 모형으로 적합시키고 나서, 오차 및 모형 분석을 통한 후에 최종적으로 2차 모형을 적합시켜 잔차 및 모형 결과를 최종적으로 검증하는 것을 시연했다.